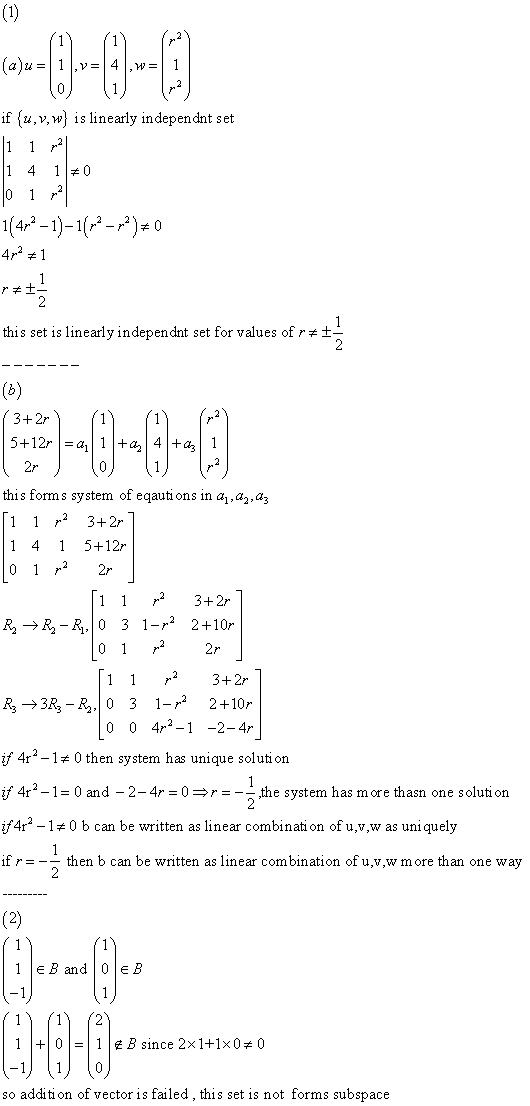Applied Mathematics 1411A/B Chapter Notes - Chapter 4.2.4: Solution Set, Scalar Multiplication, Transformation Matrix

20 views2 pages

harlequinbadger850

30 Dec 2018

School

Western University

Department

Applied Mathematics

Course

Applied Mathematics 1411A/B

Professor

Bogdan Tudose

For unlimited access to Textbook Notes, a Class+ subscription is required.

Document Summary

Theorum 4. 2. 4: the solution set of a homogenous system ax = 0 of m equations in n unknowns is a subspace of rn. Well i mean i guess that makes sense as the solution to the matrix can be added or scalar multiplied so like it"s verified. Becuase the solution set of a homogeneous system in n unknowns is actually a verified subspace of rn, we will generally refer to it as the solution space of the system. So basically, the solution of a matrix is a subspace of rn. "only systems of the form ax=0 (we call them homogeneous when the right side is the zero vector) "obviously" have a solution (apply a to 0, get 0 back), and it"s only in this case that we even use the term trivial solution, and we only call the "obvious" solution x=0=(0,0,0) x=0=(0,0,0) trivial. "

Related Questions

Show transcribed image text

scarletmallard305

I have the answer for the following question. But some of theanswers are not correct.

Please do the following question by yourself and check which arethe wrong answers,please post your answers and compare to it.

Let r in and u =(1 1 0), v = (1 4 1), w = (r2 1 r2), b = (3+2r 5+12r 2r). For which values r in is the set {u. v, w} linearly independent? For which values r in is the vector b a linear combination of u. v and w? For which of these values of r can b be written as a linear combination of u. v and w in more than one way? The set 3 of all column vectors of length three, with real entries, is a vector space. Is the subset B = {(x y z) in 3 | xy + yz = 0} a subspace of 3? Justify your answer. Show that the set of all twice differentiable functions f : satisfying the differential equation sin(x) f"(x) + x2f(x) = 0 is a vector space with respect to the usual operations of addition of functions and multiplication by scalars. Here, f" denotes the second derivative of f. Let S be the following subset of the vector space 3 of all real polynomials p of degree at most 3: S = {p in 3 | p(l) = 0, p'(l) = 0}, where p' is the derivative of p. Determine whether S is a subspace of 3. Determine whether the polynomial q(x) = x - 2x2 + x3 is an element of S. u = (1 1 0), v = (1 4 1), w = (r2 1 r2) if {u, v, w} is linearly independent set 1(4r2 - 1)-1(r2 - r2) ne 0 4r2 ne 1 r ne plusmn1/2 this set is linearly independent set for values of e ne plusmn1/2 - - - - - - - (3+2r 5+12r 2r) = a1 (1 1 0) + a2 (1 4 1) + a3 (r2 1 r2) this forms system of equations in a1, a2, a3 if 4r2 - 1 ne 0 then system has unique solution if 4r2 - 1 = 0 and -2 - 4r = 0 rArr r = -1/2, the system has more than one solution if 4r2 - 1 ne 0 b can be written as linear combination of u,v,w as uniquely if r = -1/2 then b can be written as linear combination of u,v,w more than one way - - - - - - - - - (1 1 -1) in B and (1 0 1) in B (1 1 -1) + (1 0 1) = (2 1 0) not in B since 2times1+1times0 ne 0 so addition of vector is failed, this set is not forms subspace consider the following differential equation (sinx)f"(x) + x2f (x) = 0 each solution is continuous function the set of all solutions is subset of space of set of all continuous functions n from R to R let f,g are two solutions (sinx)f"(x) + x2f (x) = 0 (sinx)g"(x)+x2g(x) = 0 ccheck whether af+bg is solution or not (sinx)f"(x) + x2f(x) = 0 rArr (sinx) af"(x) + x2?f (x) = 0 (sinx)g"(x) + x2g (x) = 0 rArr (sinx)bg" (x) + x2bg (x) = 0 (sinx)(af"(x)+bg"(x)) +x2 (af (x) + bg(x)) = 0 af+bg is also solution to differential equation the set of all solutions to differential equation forms subspace - - - - - - - - - - consider the following subset of P3 {p in P3/.p(l)=0, p'(l) = 0} let p, q in S rArr p(l)= 0, p'(l) = 0 and q(l) = 0, q'(l) = 0 (ap + bq) (l) = ap (l) +b q(l) = a (0) + b (0) = 0 (ap + bq)'(1) = ap'(l) +bq'(1) = a (0) + b(0) = 0 p, q in S rArr ap +bq in S then S is subspace q(x) = x - 2x2 + x3 q(1) = 1 - 2 + 1 = 0 q'(x)=1 - 4x + 3x2 q'(l) = 1 - 4 + 3 = 0 q is element of S

Applied Mathematics 1411A/B Chapter Notes - Chapter 4.2.4: Solution Set, Scalar Multiplication, Transformation Matrix

Document Summary

Get access

Related Documents

Applied Mathematics 1411A/B Chapter Notes - Chapter 4.7.1: Row And Column Spaces, Coefficient Matrix, Random Matrix

Applied Mathematics 1411A/B Lecture Notes - Lecture 11: Feasible Region, Linear Combination

Applied Mathematics 1411A/B Chapter 4.7.2: Applied Mathematics 1411A/B Chapter 4.7.: Applied Mathematics 1411A/B Chapter 4.7: Applied Mathematics 1411A/B Chapter 4.: Section 4.7.2

Related Questions