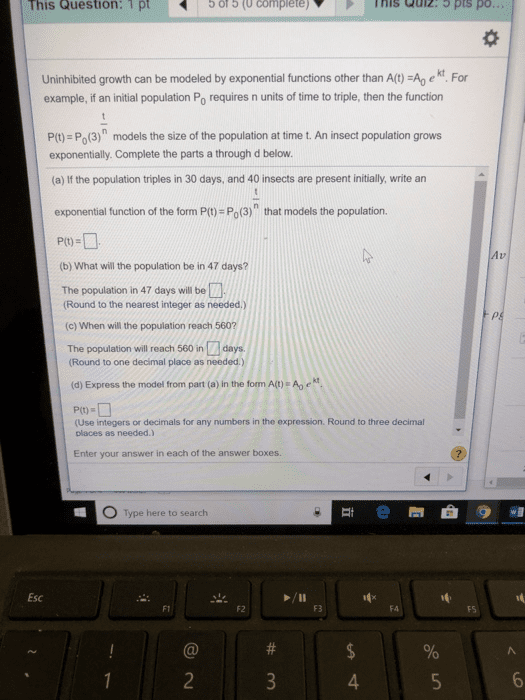
MATH135 Chapter : FLT Propositions & Complex Numbers Propositions

• School: University of Waterloo
• Department: Mathematics
• Course: MATH135
• Professor: Mike Eden

Document Summary

If and are integers, not all zero, and , then. The three integers and are a pythagorean triple if and only if the three integers are a pythagorean triple. and. If and are a pythagorean triple, then one of the integers or is even and the other is odd. If and , then there exist integers and so that and. If then there exists an additive inverse of , written with the property that. If then there exists a multiplicative inverse of , written , with the property that . If and are complex numbers, then if and only if. If and are two complex numbers in polar form, then. If is the polar form of a complex number , then the solutions to are. For all complex polynomials with , there exists a so that. If and are real (complex) polynomials and is not the zero polynomial, then there exist unique real (complex) polynomials and such that where or.