MATH 2850 Quiz: MATH 2850 Iowa 2850 Sp 2017 Solution to Quiz 1
Document Summary
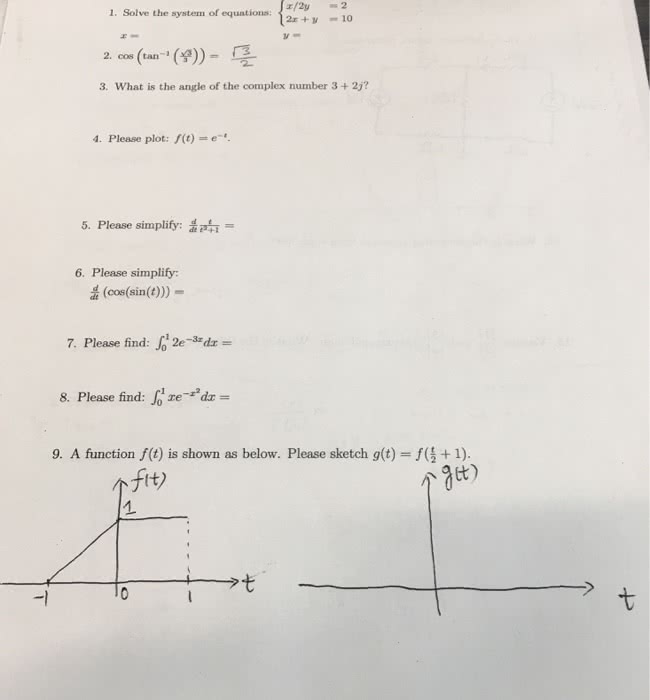
The wronskian of e tcos(t), e tsin(t) is w (e tcos(t), e tsin(t)) = Solve t dy dt + y = 8t2. Solve (3x4 + 2y)dx + (2x + 4y3)dy = 0. 4y = 30e3t + 8t, y(0) = 0, y (0) = 6, y (0) = 16. Find all equilibrium solutions and determine whether the critical point is asymptotically stable, stable, or unstable. Also classify it as to type (nodal source, nodal sink, saddle point, spiral source, spiral sink, center). Given the recursive relation an = 4an 1 (n+1)n where a0 = 1, use induction to prove that an = 4n (n+1)!n! Given the di erential equation: xy + 4y = 0. Show that x = 0 is a regular singular point of the above di erential equation. After plugging in the larger root, the recurrence relation is. For the larger root, if a0 = 1, then a1 = a2 =