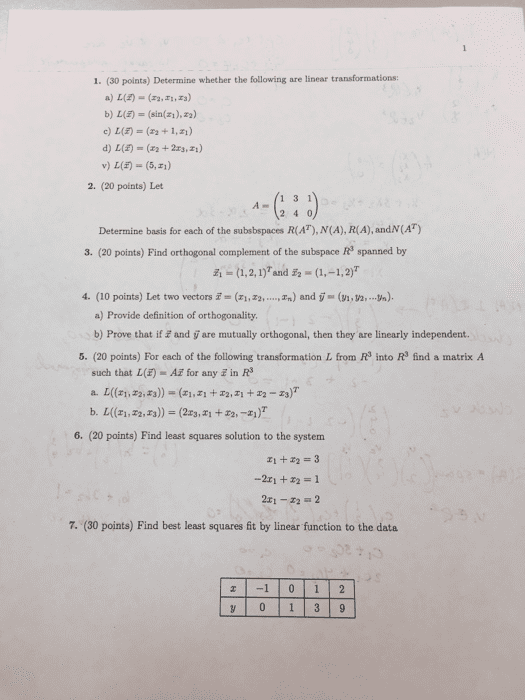MATH 235 Final: MATH 235 UMass Amherst practice-final06
Document Summary
Practice test 2: (20 points) let ~v1 = Prove that ~v1 is not perpendicular to ~v2. Find an orthonormal basis for v : (17 points) find the quadratic polynomial p(t) = a + bt + ct2 that best (in the least squares sense) ts the following data. t 1. 3: (28 points) let v c be subspace spanned by {ex, xex, x2ex}. B = (ex, xex, x2ex): (4 pts) what is the dimension of v , (8 pts, (8 pts) a matrix with respect to the basis b. i. e. compute matb. Let d : v v be the linear transformation given by d(f ) = f . Consider the function f (x) = 2ex 13xex + 2x2ex. A3 3a2 + 3a 1 = 0. f 3f + 3f f : (8 pts) Suppose you want to nd functions u such that u (x) 3u (x) + 3u (x) u(x) = x. Verify that u(x) = x 3 is a solution.