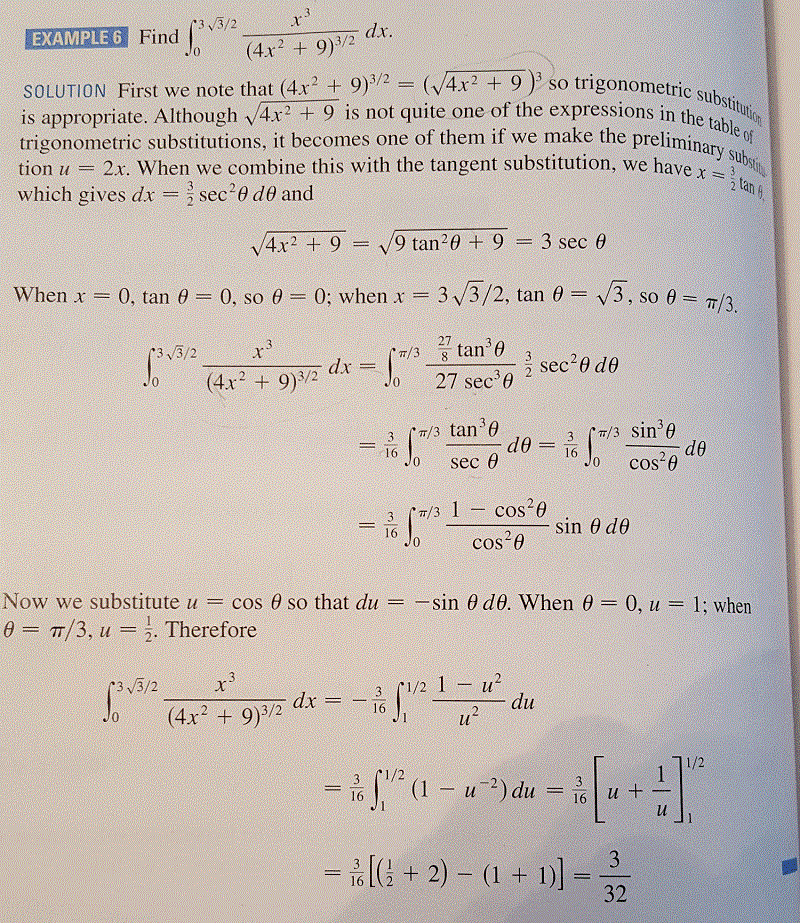MATH 132 Midterm: MATH 132 UMass Amherst math132_spring06_html solution-exam2

22 views3 pages

turquoisegnu128

31 Jan 2019

School

Department

Course

Professor

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

I :=z 1 9x2dx =z r1 . 3z 1 + cos(2 ) cos( ) = 1 9x2. d = [arcsin(3x) + 3x 1 9x2] + c = Proceed using the identities sin(2 ) = 2 sin( ) cos( ), sin( ) = 3x, and. Exam 2 solution: (16 points) for each of the following improper integrals, determine if it converges. Otherwise, explain why it or diverges. diverges: the integral is divergent. Substitute u = 1 + x2 to get: x. 0: using integration by parts, with u = ln(x) and dv = x 2dx, we get that the integral is convergent. lim t . [ln(t) ln(1)] = . ln(x) x2 dx = lim. + ln(1)(cid:21) (cid:20) 1 t 1(cid:21)(cid:27) l hopital. = [0 + 0] [0 1] = 1. 2. (a) (12 points) use the trigonometric substitution x = 1. + c (b) (3 points) the area enclosed by the ellipse 9x2 + y2 = 1.

Related Questions

Need help with convergent/divergent integrals see pictures please!

Hello, I am having an extremely diffucult time understanding trig subs in Calc2. Can someone please fully expalin to me why the limits of integration change from 3sqrt3/2 to pi/3?....and than change once again from 1 to 1/2. I know you can plug the number somewhere to see if they change, but I'm not sure where to do this...or even WHY to do this? I still don't understand why we change limits of integration in other calc problems like u-sub. Can you please explain it like you're explaining it to someone who has no math skills. I really appreiciate a clear explanation without too much math terminology.

God bless and thank you!

1. (45 marks) Short-Answer Questions. Put your answer in the box provided but show your work also. Each question is worth 3 marks, but not all questions are of equal difficulty. Full marks will be given for correct answers placed in the box, but at most 1 mark will be given for incorrect answer. Unless otherwise stated, it is not necessary to simplify your answers in this question. a) Find the equation of the tangent plane to the graph of the function z = f(x,y) = sell at (0,1). Answer b) Evaluate (T, 0) if f(x,y) = sin(ry). Answer c) Graph of a function z = f(x,y) is given by: Which of the following level curves correspondes to this function. Answer d) If f(x,y) = e(3x – 2y), find lim - Math)-f(x,y) e) Find % if f(x, y) = x2 - y3 and 2 = r sin(t), y = r cos(t). Answer f) Evaluate the directional derivative of f(x, y) = !at (1, -1) in the direction of u =(2, 1). Answer 8) Does Simono converge? h) Sketch the direction field of the differential equation = 1-2y. i) Consider the differential equation ay = 15 - 31, y(0) = 0, and use Euler's method with step size 0.1 to estimate y(0.1). Answer j) Knowing that (-3,-3) is a critical point of f(x,y) = 2:3 + y2 – 4.cy -3.0, use the second derivative test to find out whether it is a local minimum, local maximum, or a saddle point. Answer k) Solve the initial value problem, dy dt 642 2y + cos(u) y(1) = . Answer 1) Is ū=(2,2, -1) perpendicular to v = (5,-4, 2)? Answer m) Find the area between the graph of y = 1 + sin(x) and y=1-sin(x) from 0 to 7. Answer n) Determine the lentgh of the curve y = 8/2,0 SIS 3. Evaluate and simplify your answer. Answer o) Express the volume of the solid obtained by rotating the bounded region that lies between curves y = (x-2)2 and y=1,150 $4 about the vertical line 2 = 5. Do not evaluate this integral. Answer

MATH 132 Midterm: MATH 132 UMass Amherst math132_spring06_html solution-exam2

Document Summary

Get access

Related textbook solutions

Calculus

Single Variable Calculus: Early Transcendentals

CALCULUS:EARLY TRANSCENDENTALS

Related Documents

MATH 132 Midterm: MATH 132 UMass Amherst Math-132-Exam-1-SP16

MATH 132 Midterm: MATH132 Exam 1 2015 Spring Solution

MATH 132 Final: MATH 132 UMass Amherst math132_spring06_html final-compressed

Related Questions