MATH 132 Midterm: MATH132 Exam 3 2007 Spring Question 2

Math 132 Exam 3 Practice Problems Spring 2007
1. Does the series converge? Why or why not? (Name any test you use and show that the
conditions needed for that test are satisfied.)
(a) 1
5−3
25 +9
125 −27
625 +···
(b)
∞
n=1
3n7
8n7+6n2−5n−2
(c)
∞
n=1
√n3+2n
n4−7
(d)
∞
n=1
(−1)nn3−n
4n5+n3+4
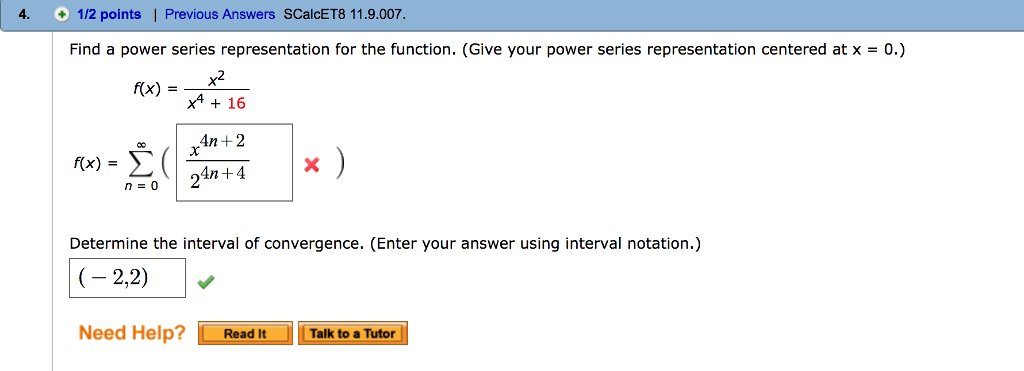
2. (a) Find the interval of convergence of the power series
∞
n=0
(x−1)n
(n+ 1)3n.
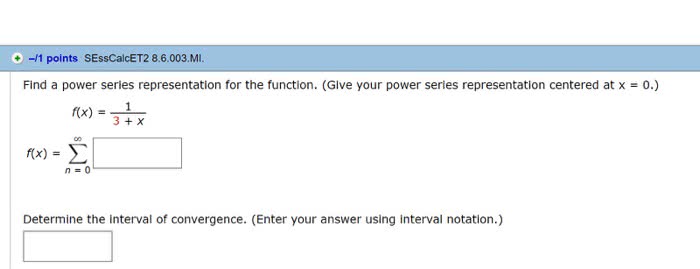
(b) Find a power series representation for f(x)= 4
1+2xaround a= 0; write the power
series using sigma () notation. State for which xthe power series actually has
sum f(x).
3. The sequence {Sn}∞
n=1 of partial sums of the series
∞
n=1
anis given by
Sn=n
5+nfor n=1,2,3,...
(a) Does the series
∞
n=1
anconverge? If so, to what sum?
(b) Use the formula for Snto find the values of a1and a2. Then find an explicit formula
in for anin terms of n.
4. Consider the power series
∞
n=1
(−1)n−1
(n+ 1)! xn.
(a) Determine the radius of convergence of this power series.
(b) Show that this power series converges for x=1
3.
(c) How many terms do you need to use to approximate the infinite series in (b) so that
the error is less than 0.001?
5. Find the first three terms of the Taylor series for the function f(x)=xln(x2+1) centered
around a=1.
6. (a) Starting with the MacLaurin series for ex(which you may just write down), obtain
a power series representation of e−x2.
(b) Use your answer to (a) to express 1
0
e−x2dx as the sum of an infinite series.
(c) Find a bound on the error if the first three terms of the series you obtained in (b)
were used to approximate 1
0
e−x2dx. (Do not actually calculate the approximation
and do not use any value for this integral that your calculator might give.)
Document Summary
Why or why not? (name any test you use and show that the conditions needed for that test are satis ed. ) 8n7 + 6n2 5n 2 n3 + 2n n4 7 ( 1)n n3 n. 4n5 + n3 + 4 (b) (c) (d) n=1. 2. (a) find the interval of convergence of the power series. (cid:2) n=0 (x 1)n (n + 1)3n . (cid:2) n=1 an is given by (b) find a power series representation for f(x) = 4 (cid:3) 1+2x around a = 0; write the power. State for which x the power series actually has series using sigma ( sum f(x): the sequence {sn} n=1 of partial sums of the series (a) does the series. If so, to what sum? (b) use the formula for sn to nd the values of a1 and a2. Then nd an explicit formula in for an in terms of n.