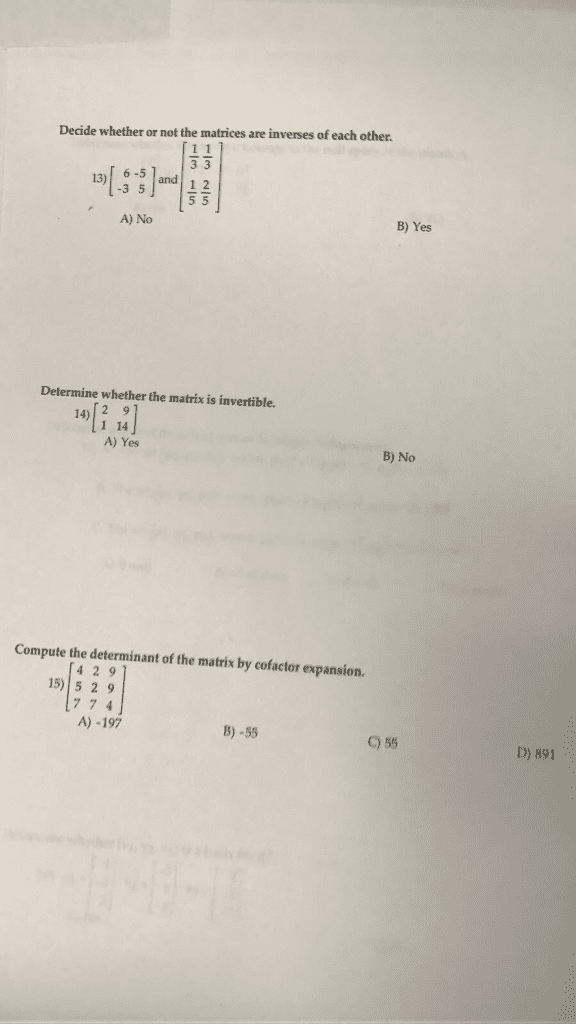MATH 131 Midterm: MATH 131 UMass Amherst Umass_Exam2_2016
Document Summary
Practice quiz 5: use gauss-jordan elimination to nd the determinant of the matrix a , let a and b be two 5 5 matrices, with det a = 0 and det b = 3. Why, or why not? (e) compute det (b a b). (f) compute det (b )3. (g) compute det (2b): find a 2 2 matrix a such that (cid:20) 2. 5(cid:21) are eigenvectors of a, with eigenvalues 7 and. If yes, compute its diagonalization d. if not, explain why not: let a = . 0 (a) find the eigenvalues of a. (b) find a basis for each eigenspace of a. (c) find a diagonal matrix d and an invertible matrix s such that a = s d s 1. If not, say so. (c) compute det (4a). (d) compute det (a4). 0 5(cid:21): which of the following 2 2 matrices is similar to the matrix d = (cid:20)2 0.