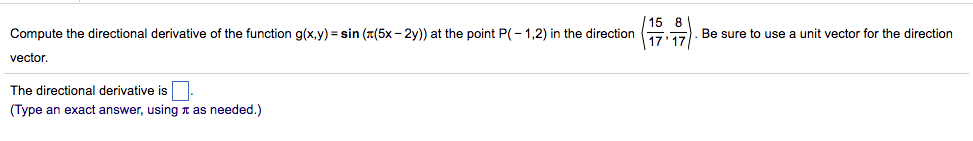MATH 215 Final: finalf14
Document Summary
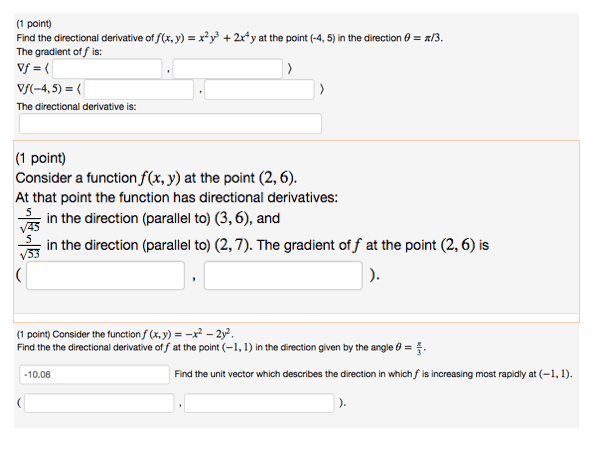
Fall 2014, math 215 calculus iii, final exam. 12/12/2014, 10:30am 12:30pm (120 minutes: (10 point) let f (x, y, z) be a function which has continuous partial derivatives. Find the gradient of f at p (1, 2, 3): (5 point) a particle is moving in space. It starts o at the origin with initial velocity ~i ~j + 3~k. The curved part of c is a portion of a circle centered at (0, 0). Evaluate the work done by the vector eld in moving a particle along c. C (0,0) x (-1,-1) (1,-1: (10 point) let. ~f (x, y, z) = hx2, 2xy + sin z, zi. Evaluate the ux of the vector eld ~f across the boundary surface of the unit cube, given with positive (outward) orientation, in the picture. z. 1 x: (10 point) let c be the part of the curve x + y2 = 4 from point ( 5, 3) to point (0, 2).