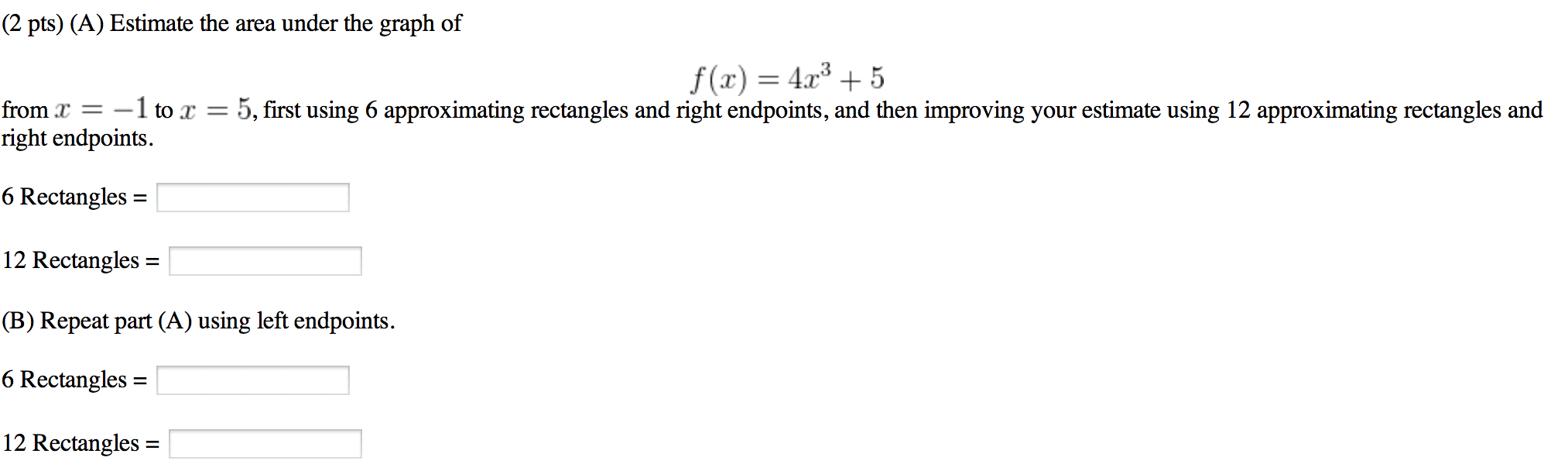MATH 2B Study Guide - Quiz Guide: Antiderivative

• School: UC-Irvine
• Department: Mathematics
• Course: MATH 2B
• Professor: All

Document Summary

Cross out incorrect scratch-work: no calculators or other forms of assistance are allowed. 3x2 1 dx (cid:90) 1 sin2(x) cos x b. dx: (cid:82) sin(7 + 5) d , (15 points, find the average value of the function f (x) = tan3(x) sec2(x) on the interval [0, . 4 ]: a particle moves along a line so that its velocity at time t is v(t) = |2 t|. Find the displacement of the particle during the time period 0 t 3: (20 points, complete the blanks in the following statement of the fundamental theorem of calculus. and. If g(x) = (cid:82) x (cid:82) b a f (x) dx = a f (t) dt, then g(cid:48)(x) = , where f is any antiderivative of f: use the fundamental theorem of calculus to evaluate the following. (cid:90) y. 2: d dy sin(t) t2 + 3 dt (cid:90) x4 x t dt, d dx, answer each of the following questions.