MA 125 Midterm: 16-Spring-Ex2_-_Cal_I
Document Summary
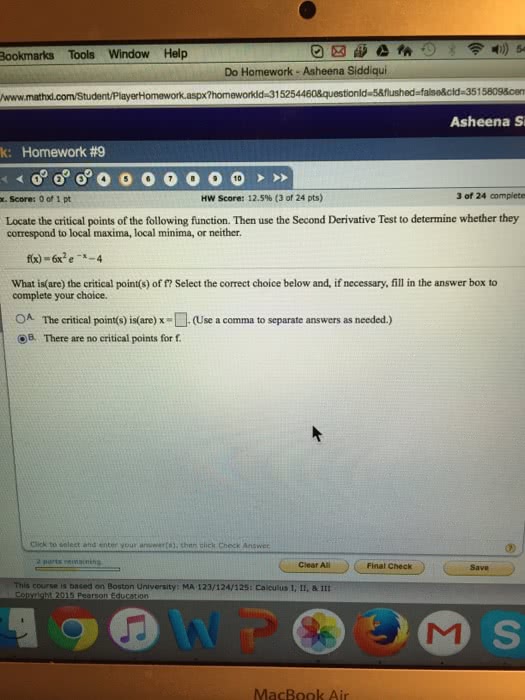
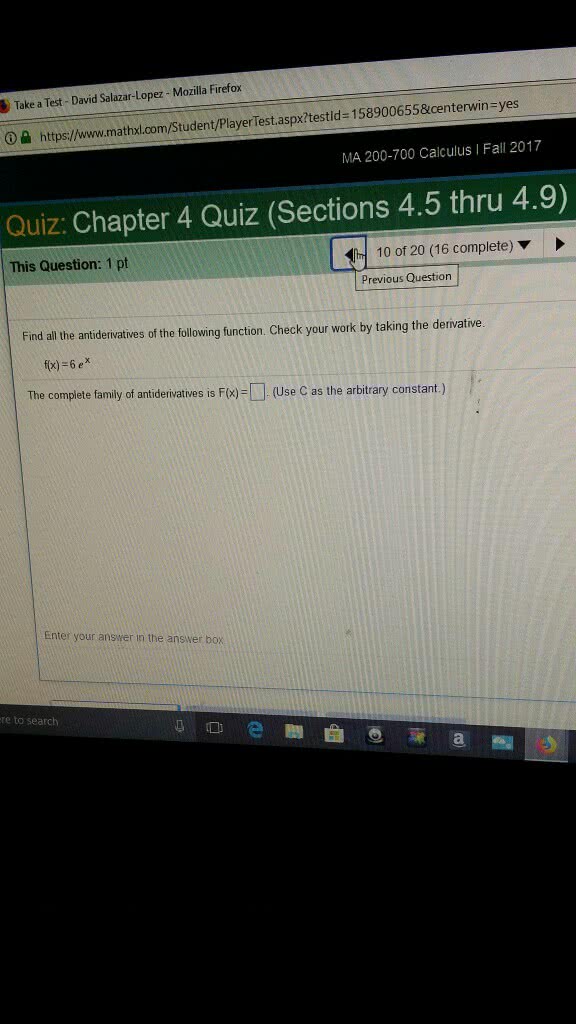
Show all your work, simplify and justify your answer! No partial credit will be given for the answer only! All problems in part i are 10 points each: find the derivative of the function f (x) = (cid:0)x3 + x(cid:1)5, find all critical numbers of the function f (x) = (2x + 1)3(1 x)7. 2: find the absolute maximum and minimum of the function f (x) = x4. 2x2 on the interval [ 2, 2]: verify that the conditions of the mean value theorem hold. Next nd the number c which satis es the conclusion of the mean value theorem for the function f (x) = x5 on the interval [0, 1]. 3: show that the equation f (x) = x7 + x3 + x + 5 = 0 has exactly one solution. Hint: rst show that there is at least one solution. Next show that two distinct solutions is impossible.