MATH 110 Study Guide - Final Guide: Good Luck!!, Differentiable Function, Antiderivative
University of San Francisco
MATH 110
Calculus & Analytic Geometry II
Spring 2018
Final Exam
Prof: Stephen Devlin
Exam Guide
Topics Included:
1. Curves Defined by Parametric Equations
2. Calculus with Parametric Curves
3. Polar Coordinates
4. Area and Lengths in Polar Coordinates

Chapter 10 – Parametric Equations and Polar Coordinates
10.1 Curves Defined by Parametric Equations
Parametric Equations: Equations where and are both given as functions of a third variable .
=() =()
Parametric Curve: The curve of parametric equations where each value of determines a point
(,) which can be plotted in a coordinate plane. The curve with parametric equations:
=() =()
has initial point ((),()) and terminal point ((),()).
Example A: Sketch the curve with parametric equations: =cos = sin 2
where 0
Solution:
Example B: Eliminate the parameter to find a Cartesian equation of the curve.
= =+ 2
Solution:
=2 Use the simpler equation to solve for
=() Substitute for in the other equation
ln = 3(2) Take the natural log of both sides (this cancels on the right)
ln = 36 Distribute the 3
3=ln + 6 Add 6 to both sides and reverse sides so is on the left
=
or =
+ Solve for , either equation is correct
-4 -3 -2 -1 0 1 2 3 4
2
1
-1
-2
0
1
0
1
0 1
0
1
0
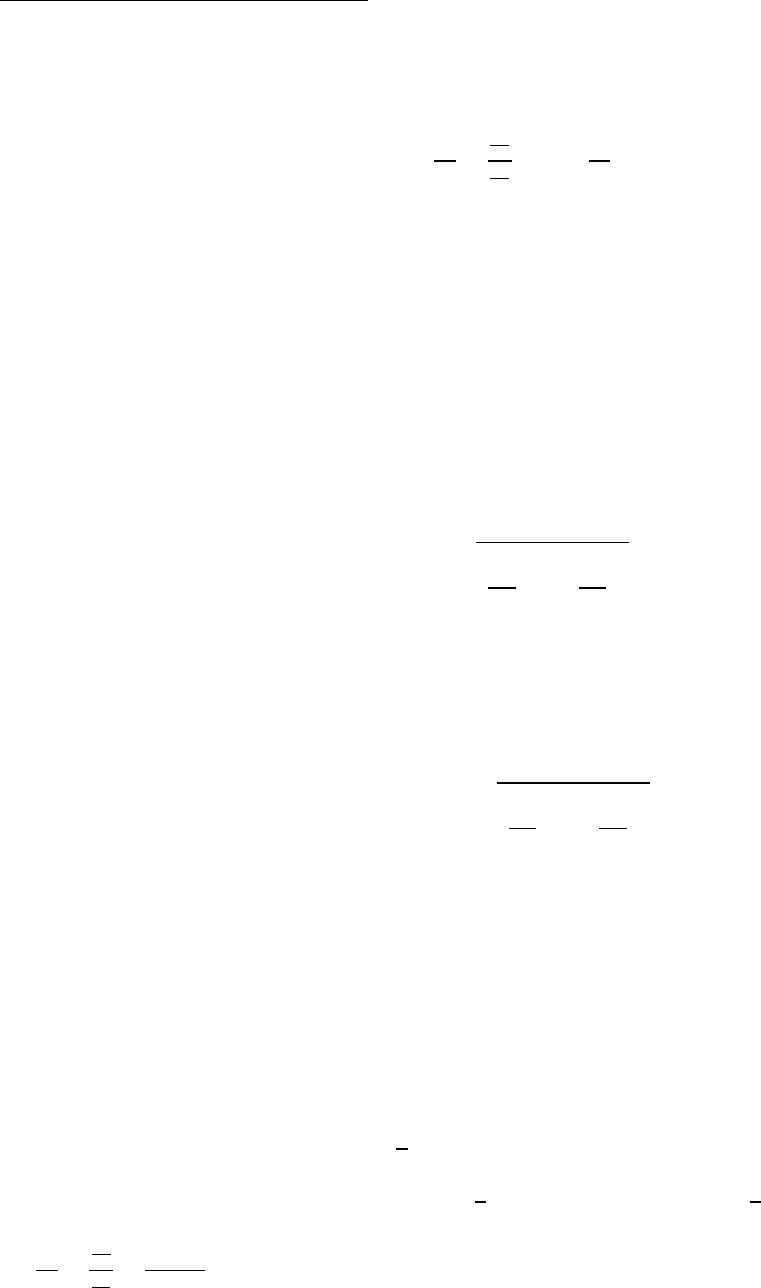
10.2 Calculus with Parametric Curves
Tangents: Suppose and are differentiable functions, the tangent line at a point on the
parametric curve =(), =(), where is also a differentiable function of .
Then
=
if
0
Areas: The area under the curve defined by the parametric equations =() and =(),
is:
= ()()
Arc Length: If a curve is defined by the parametric equations =(), =(), ,
where and are continuous on [,] and is traversed (or traced) exactly once as increases
from to , then the length of is:
=
+
Surface Area: If a curve is defined by the parametric equations =(), =(), ,
where and are continuous, ()0, and is rotated about the -axis. If is traversed (or
traced) exactly once as increases from to , then the surface area is given by:
=2
+
Example A: Find the equation of the line tangent to the curve defined by parametric equations:
=cos = sin 2 at the point (0,0)
Solution:
0 = cos =cos0=
Find when =
0 = sin 22= sin02==
Confirm that =
when =
=
=
Find the derivative to find the slope of the tangent line
Document Summary
Topics included: curves defined by parametric equations, calculus with parametric curves, polar coordinates, area and lengths in polar coordinates. Chapter 10 parametric equations and polar coordinates. Parametric equations: equations where and are both given as functions of a third variable . Parametric curve: the curve of parametric equations where each value of determines a point (,) which can be plotted in a coordinate plane. The curve with parametric equations: has initial point ((),()) and terminal point ((),()). Example a: sketch the curve with parametric equations: = cos = sin 2 where 0 . Example b: eliminate the parameter to find a cartesian equation of the curve. Take the natural log of both sides (this cancels on the right) Add 6 to both sides and reverse sides so is on the left. =3( 2) ln = 3( 2) ln = 3 6. 10. 2 calculus with parametric curves if 0.



