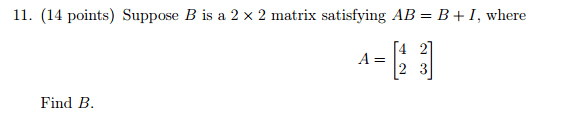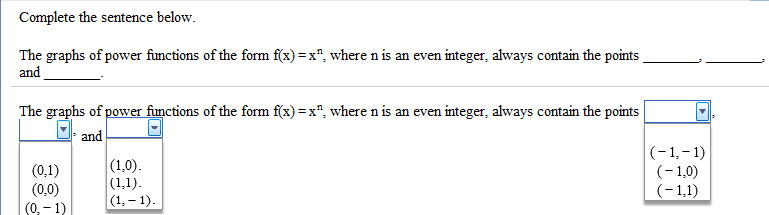MATH 432 Final: MATH432_COHEN-J_FALL2012_0101_FINAL_EXAM

• School: University of Maryland
• Department: Mathematics
• Course: MATH 432
• Professor: All

Document Summary

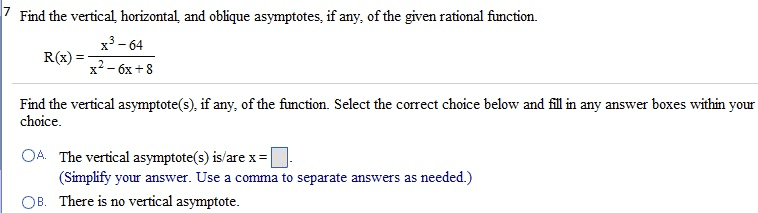
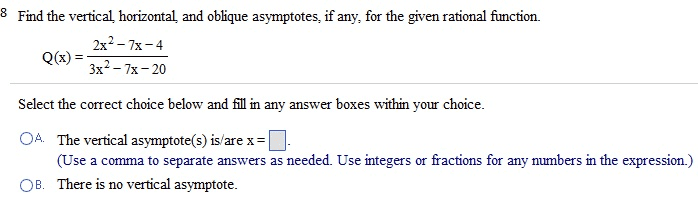
1:30-3:30: (20 points) let x be a limit point compact space. Prove each of the following statements. (a) if f : x y is continuous, then f (x) is limit point compact. (b) if a is a closed subset of x, then a is limit point compact. Math 432: (20 points) recall that a subset s of a real vector space is convex if for any x, y s, tx + (1 t)y s for all t [0, 1]. Show that any two bounded convex open subsets of r2 are homeomorphic. Hint: show that any bounded convex open subset of r2 is homeomorphic to b2 = {|z| < 1}. Math 432: (20 points) let f, g : x y be continuous where y is hausdor . {x x|f (x) = g(x)} is closed in x. 3: (20 points) let p : s 1 s 1 be given by p(z) = zn for n a positive integer.