MATH 410 Midterm: MATH410_BOYLE-M_FALL1993_0101_MID_EXAM_2

• School: University of Maryland
• Department: Mathematics
• Course: MATH 410
• Professor: All

Document Summary

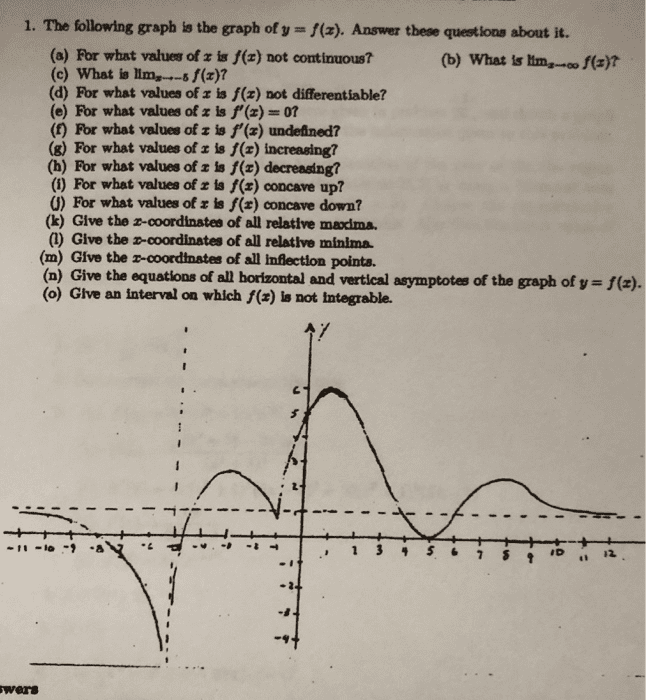
2 dx. (c) (5 points) di erentiate the function. 3 g(x) = z x x sin(t2)dt: (a) (5 points) give an example of a bounded function from [0,1] into r which is not integrable. Justify your answer. (b) (15 points) prove that a continuous function f from [a,b] into r is integrable: (15 points) prove the following fragment of the fundamental theorem of calcu- lus. Suppose f is a continuous function from [a,b] into r and f is de ned on [a,b] by. F (x) = z x a f (t)dt. F (x) f (x0) x x0. = f (x0): (15 points) suppose f is a continuous nonnegative function from [0,1] into r such that f (0) > 0.