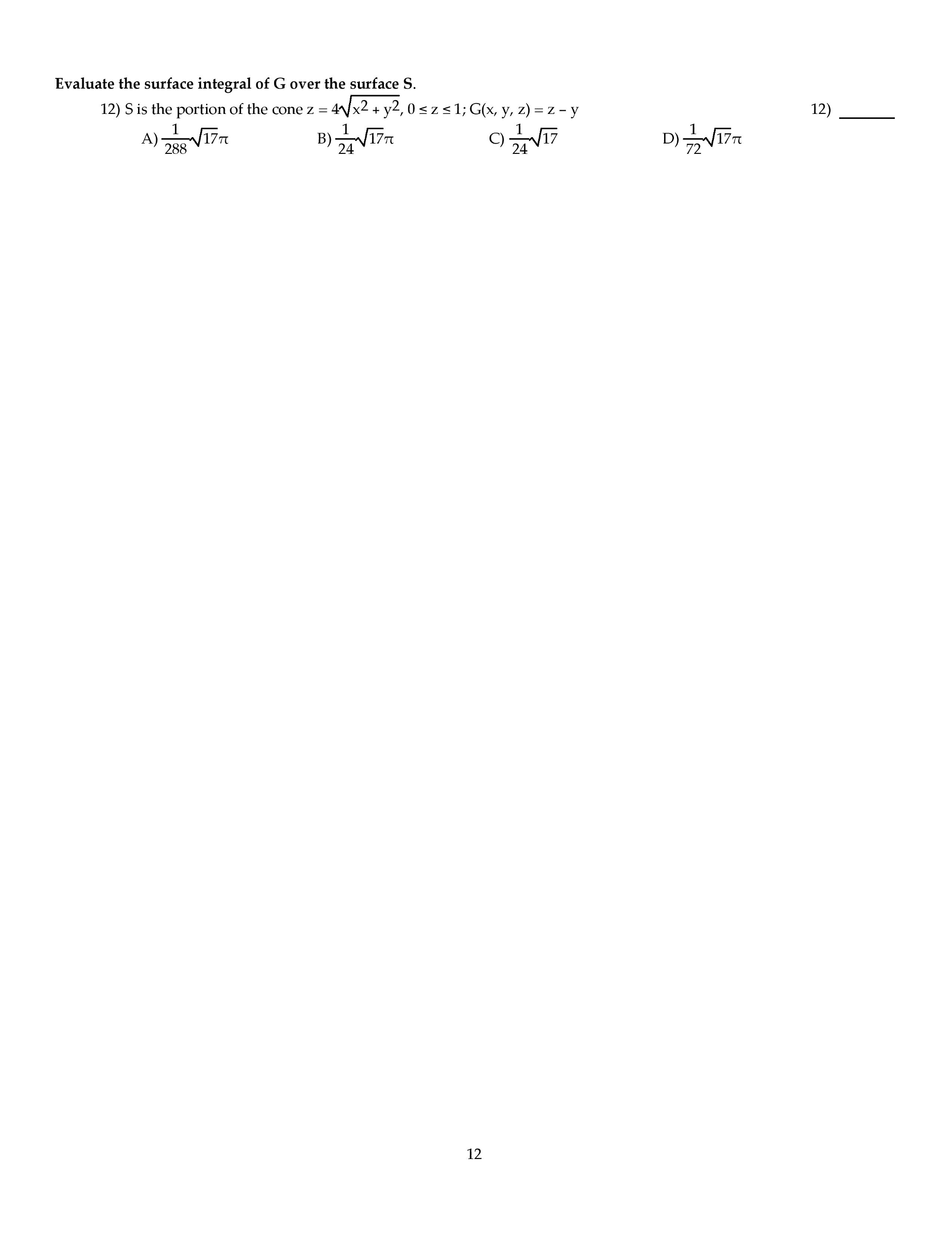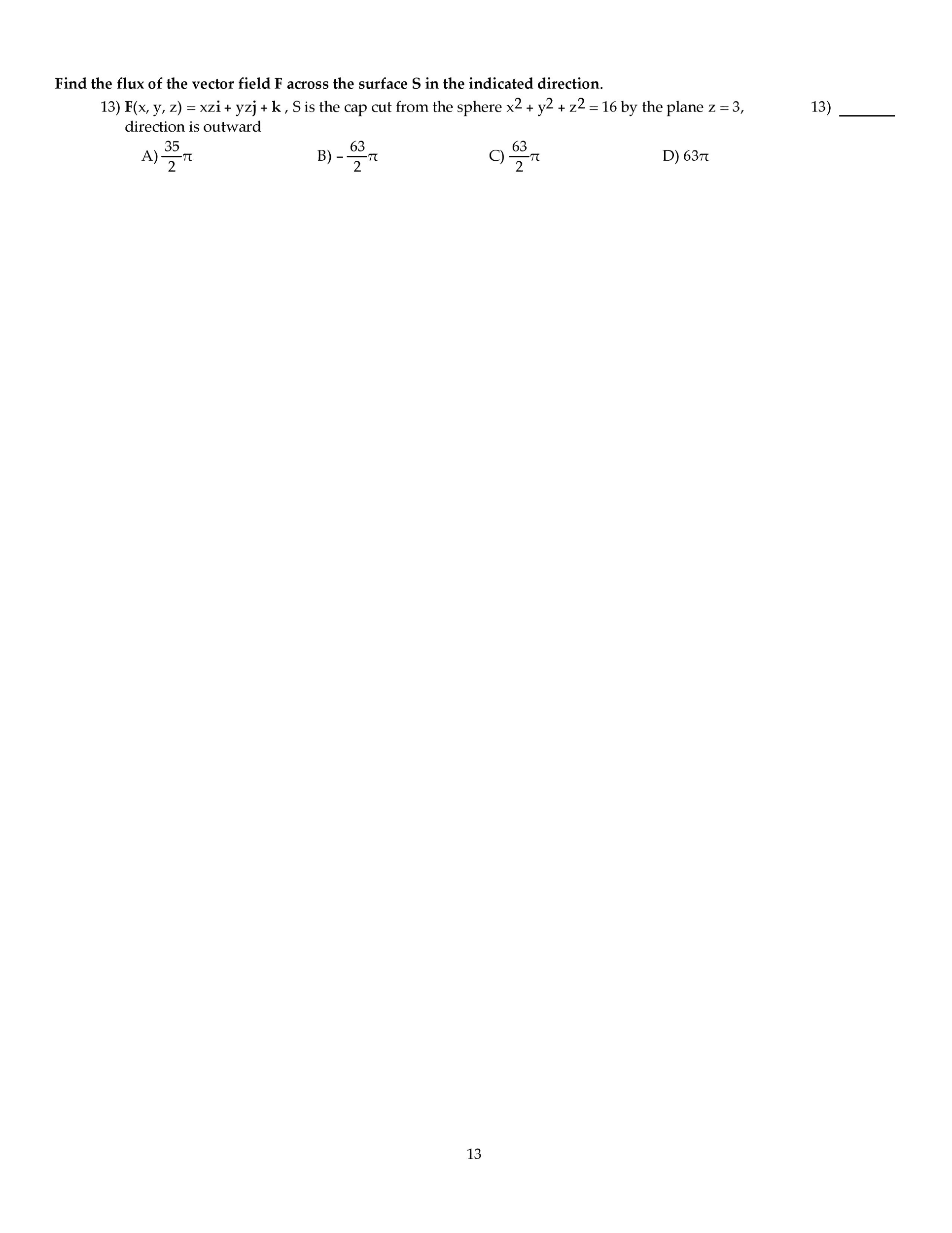Put a box around the result of a computation. Boyle summer 2005: consider the di erential equation ty + y = cos(t) , t > 0 . (a) (15 points) solve the di erential equation. Multiply both sides of the d. e. by 1/t to put it in standard form: y + (1/t)y = (1/t)cos(t) . Now multiply both sides by the integrating factor exp r 1/t = exp ln(t) = t (by coincidence recovering the original equation) to get (ty) = cos(t) . Integrate both sides to get ty = sin(t) + c, and thus the general solution y = c sin(t) + c(1/t) . (b) (5 points) describe the behavior as t 0 for various constants of integration. We write the de as m dx + n dy = 0, (yexy + 2x)dx + (xexy + cos y)dy = 0 . The de is exact if m/ y = n/ x, and this holds because.
