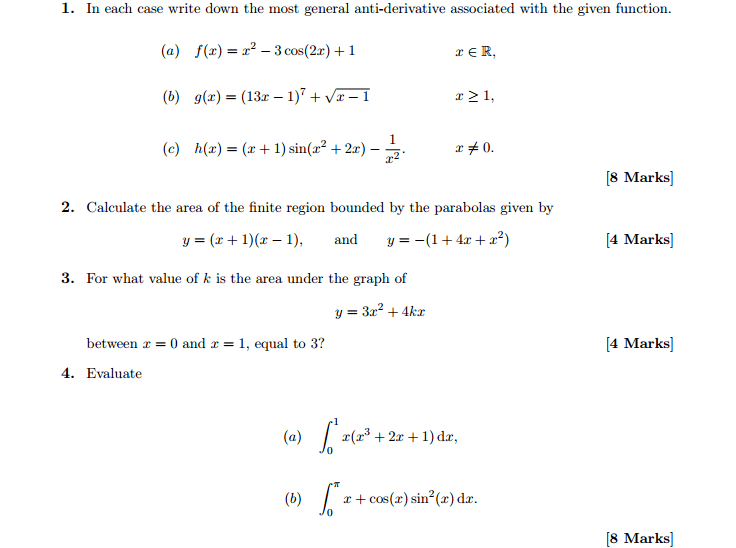MATH 152 Midterm: MATH 152 TAMU 2012c Exam 1a Solutions
Document Summary
Fall 2012 math 152: e integrate with respect to x, i. e. , top function - bot- tom function and note that these change at x = 0. Exam i version a solutions area is 0. 1 + x2 dx = 2 arctan x|1. 2 so the identity used is sin2 x : c sin2 x dx = 1. 2 sin 2x: c let u = x3 and dv = e . Apply the formula u dv = uv v du. 2 e v = to obtain . 2 x2e 2x dx: b 2 indicates that the volume is obtained using the shell method with a radius of x and height (x 3)2 0. Therefore, this solid is obtained by rotating about the y-axis the area between y = (x 3)2 and the x-axis: c let u = x2. Changing bound- integral becomes aries and noting that x2 = u, the integral becomes.