MAT 132 Midterm: MAT 132 SBU Exam Solution 1

• School: Stony Brook University
• Department: Mathematics
• Course: MAT 132
• Professor: All

Document Summary

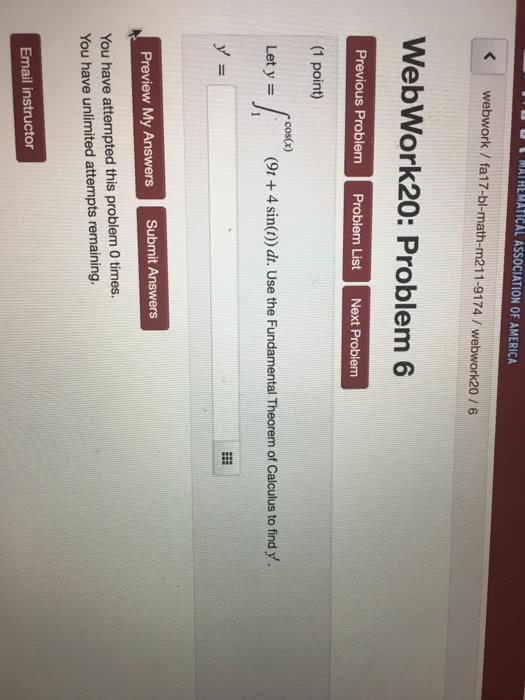
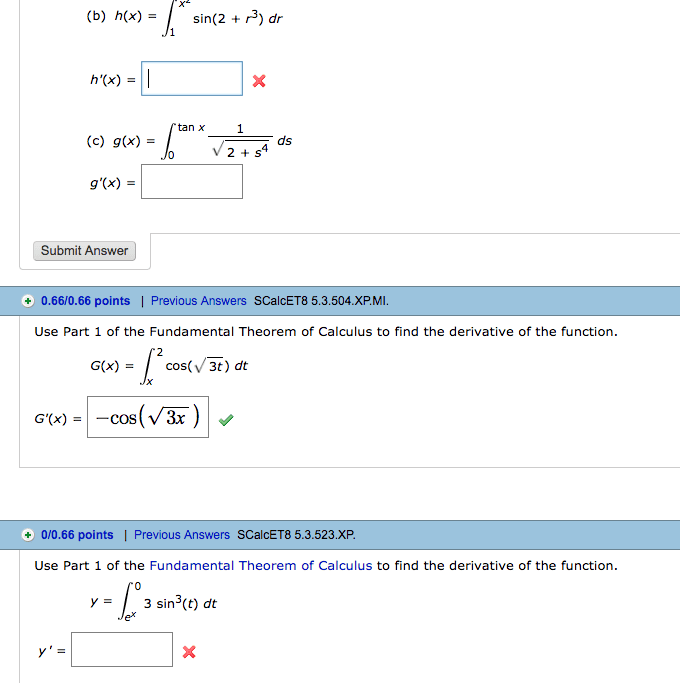
T sin3( t) + e arctan(1 t2) t and let g(x) = z x. By the fundamental theorem of calculus, we have. 0 h (t) dt = h(1) h(0) = sin3( ) + e1 arctan(0) 1 sin3(0) + e0 arctan(1) 0 e. By the fundamental theorm of calculus (the other part) we have g (0) = h(0) = . Determine whether the following integrals converge or diverge. Find the exact answer if possible. (a) z . = lim b ln(ln(b)) ln(ln(2)) = . 1 + x3 converges if z dx. 1 + x3 converges by dx dx dx dx. 3 which converges, the comparison theorem says that z . We integrate explicitly (using integration by parts): dx = lim b z . 12 (a) use the left hand rule with n = 5 to approximate z 12. Let"s denote (for this part and every part) with n = 5 gives. 8x + 3 x2 5x + 9 by f (x).