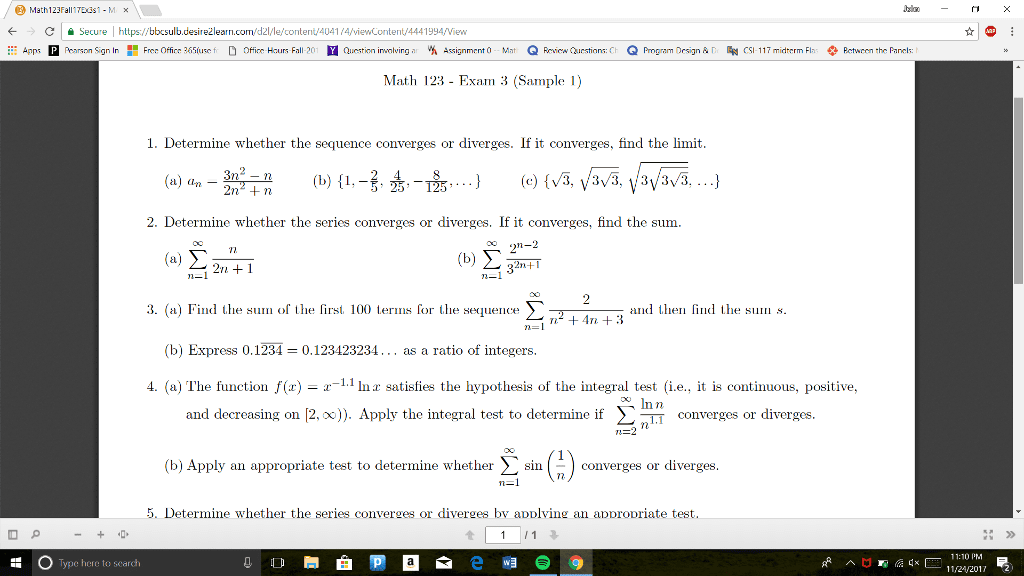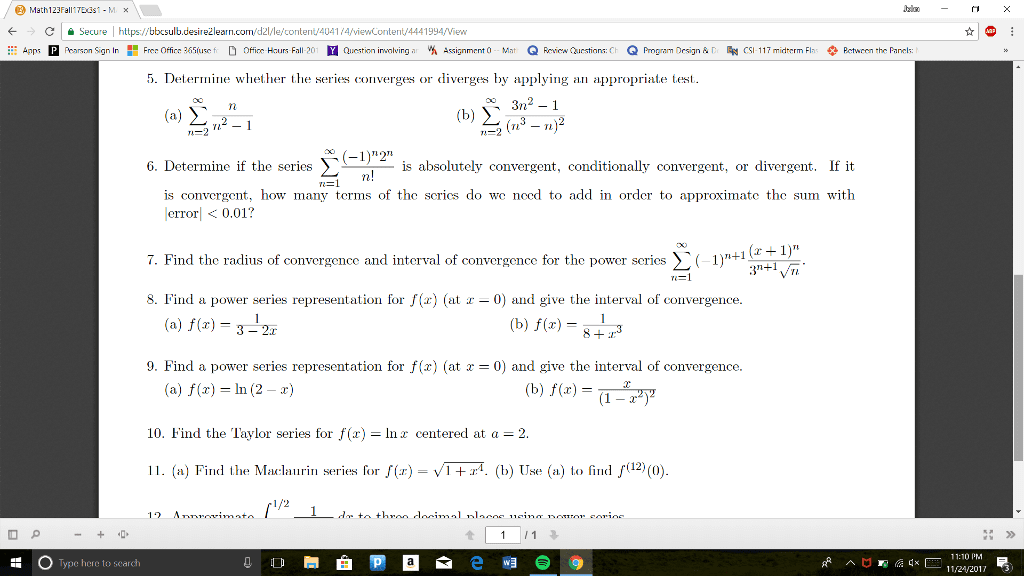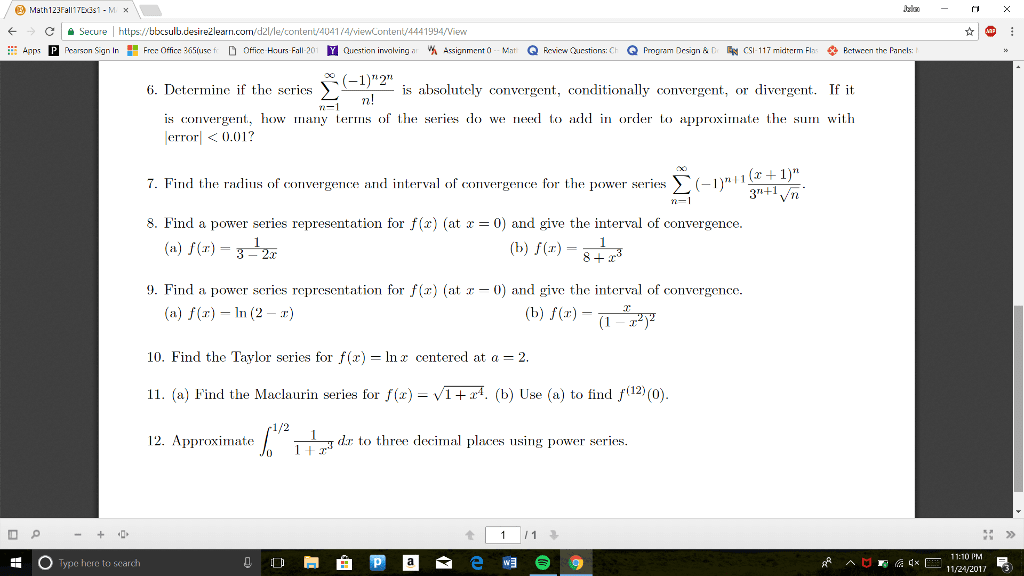MAT 132 Midterm: MAT 132 SBU Exam Midterm 2 Fall 11a Solution

• School: Stony Brook University
• Department: Mathematics
• Course: MAT 132
• Professor: All

Document Summary

Solutions to midterm 2 (papaya: for each of the following sequences, determine whether it converges or diverges. 5 pts (a) (1 + 3n)(2 + n3)(cid:27) (cid:26) 2n4 + cos(n ) n=0. Solution: for n large, the cos(n ) term is irrelevant, as are the lower powers of n in the denominator. 2n4 + cos(n ) (1 + 3n)(2 + n3) 2n is of the form / , so we can use l"h opital"s rule. 5 pts (c) n=0 = e + 1, e 1, e + 1, . Solution: the sequence diverges, because the limit as n does not exist; it alternates between e + 1 and e 1. Keep in mind that n must be a whole number. Xn=0 ( 1)n n2 + 2 is within 1/100 of the. Solution: since this is an alternating series, we know that the remainer rn is less than the absolute value of the n + 1-st term.