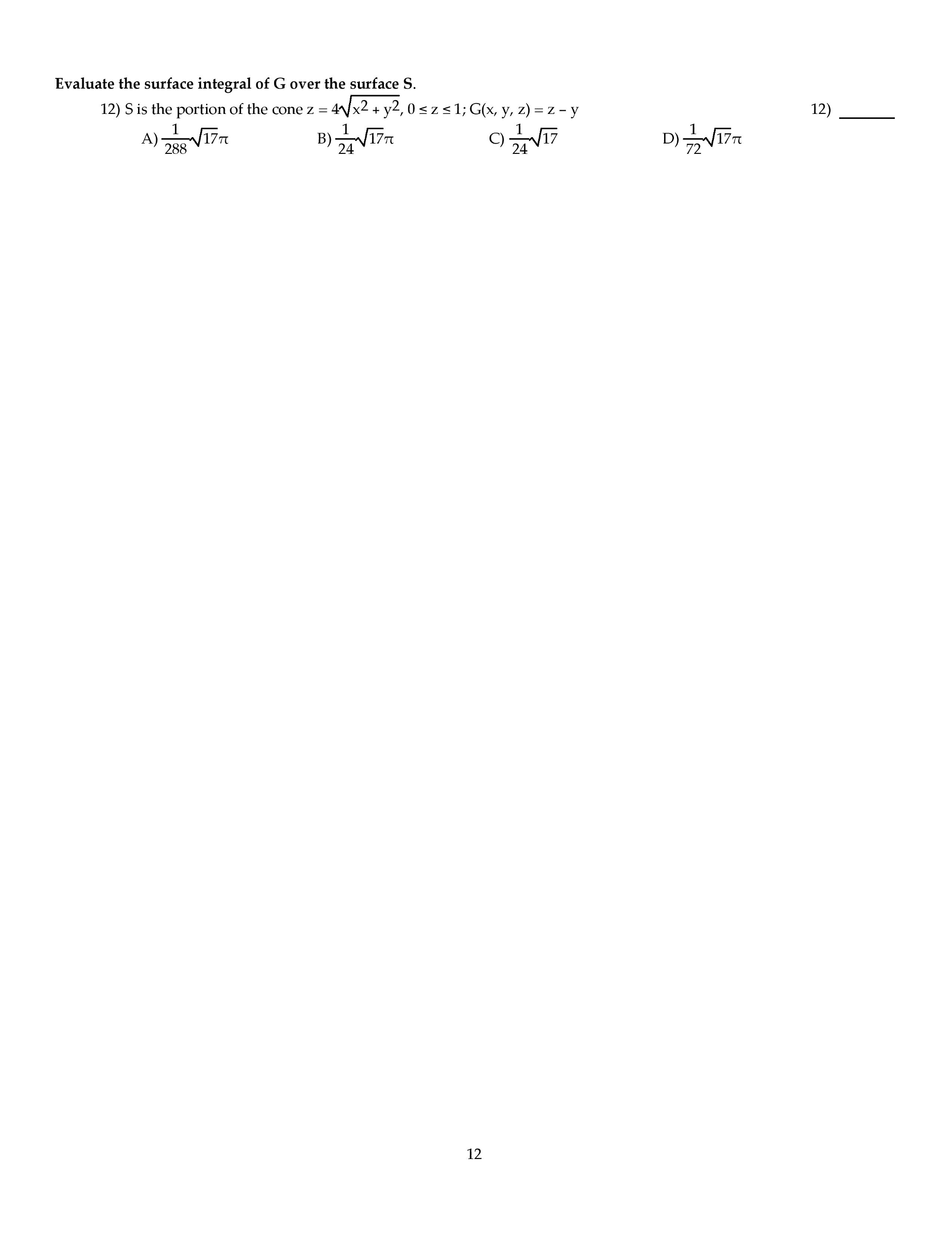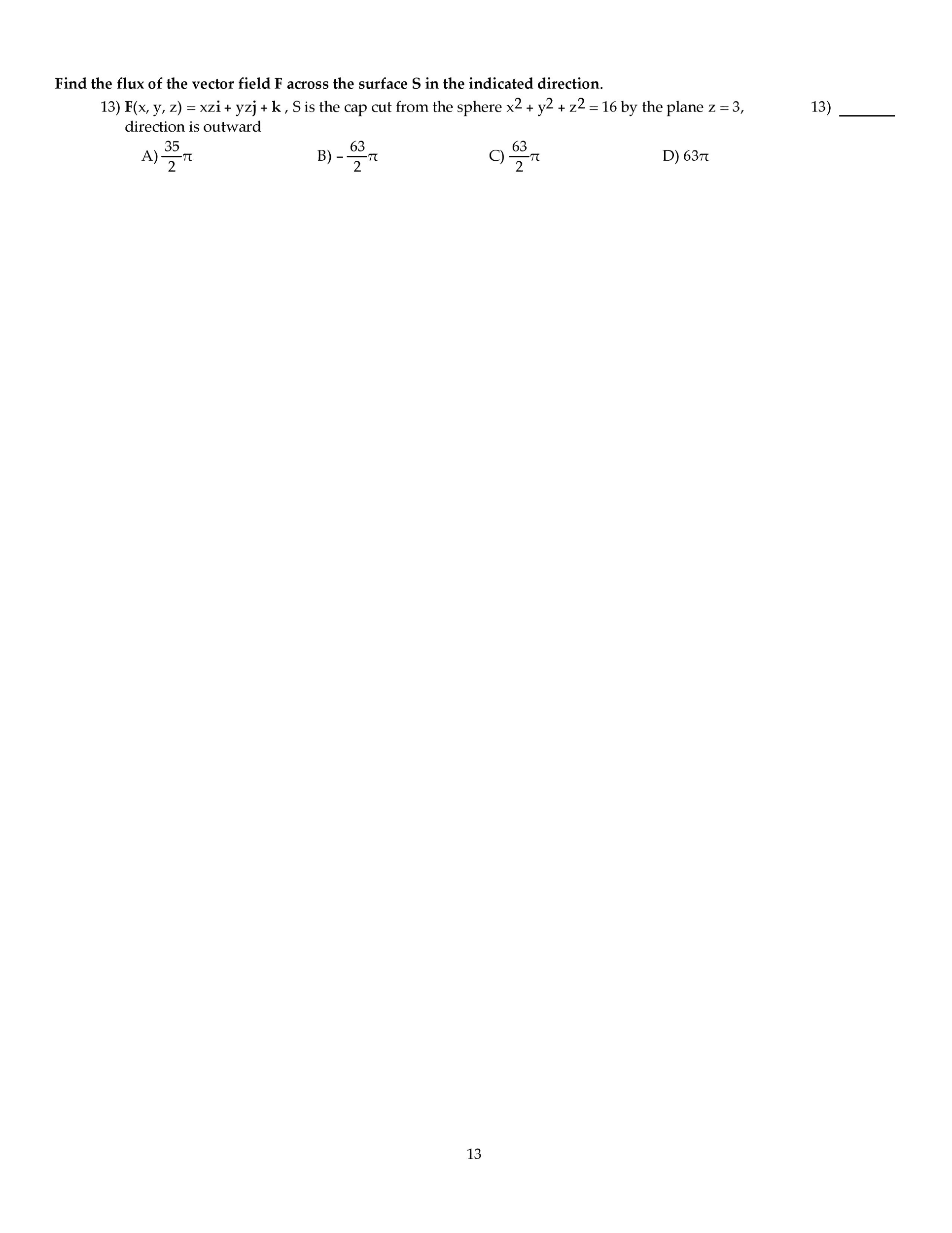MATH 142 Midterm: MATH142 South Carolina 16s2eSolution

Spring 2016 Exam 2
MARK BOX
problem points
0 20
1 20
2 10
3 10
4-7 20
8 10
9 10
%100
NAME: KEY-e-poo
PIN: 17
INSTRUCTIONS
•On Problem 0, fill in the blanks. As you know, if you do not make at least half of the points on Problem
0, then your score for the entire exam will be whatever you made on Problem 0.
•For multiple choice problems, circle your answer(s) on the provided chart. No need to show work.
•For all other problems, to receive credit you MUST show ALL your work and :
(1) work in a logical fashion, show all your work, indicate your reasoning;
no credit will be given for an answer that just appears;
such explanations help with partial credit
(2) if a line/box is provided, then:
— show you work BELOW the line/box
— put your answer on/in the line/box
(3) if no such line/box is provided, then box your answer.
•Upon request, you will be given as much (blank) scratch paper as you need.
•Check that your copy of the exam has all of the problems.
•During the exam, the use of unauthorized materials is prohibited. Unauthorized materials include: elec-
tronic devices, books, and personal notes. Unauthorized materials (including cell phones) must be in a
secured (e.g. zipped up, snapped closed) bag placed completely under your desk or, if you did not bring
such a bag, given to Prof. Girardi to hold for you during the exam (and they will be returned when you
leave the exam). This means no electronic devices (such as cell phones) allowed in your pockets. At a
students request, I will project my watch upon the projector screen.
•During this exam, do not leave your seat unless you have permission. If you have a question, raise your
hand. When you finish: put your pencil down and raise your hand.
•This exam covers (from Calculus by Thomas, 13th ed., ET): §10.1–10.6 .
Honor Code Statement
I understand that it is the responsibility of every member of the Carolina community to uphold and
maintain the University of South Carolina’s Honor Code.
As a Carolinian, I certify that I have neither given nor received unauthorized aid on this exam.
I understand that if it is determined that I used any unauthorized assistance or otherwise violated the
University’s Honor Code then I will receive a failing grade for this course and be referred to the academic
Dean and the Office of Academic Integrity for additional disciplinary actions.
Furthermore, I have not only read but will also follow the instructions on the exam.
Signature :
Prof. Girardi Page 1 of 11 Math 142

Spring 2016 Exam 2
0. Fill-in-the boxes. All series Pare understood to be P∞
n=1 , unless otherwise indicated.
0.1. Geometric Series. Fill in the boxes with the proper range of r∈R.
•The series Prnconverges if and only if rsatisfies |r|<1 .
0.2. p-series. Fill in the boxes with the proper range of p∈R.
•The series P1
npconverges if and only if p > 1.
0.3. State the Integral Test for a positive-termed series Pan.
Let f: [1,∞)→Rbe so that
•an=f(n) for each n∈N
•fis a positive function
•fis a continuous function
•fis a decreasing (nonincreasing is also ok) function.
Then Panconverges if and only if Rx=∞
x=1 f(x)dx converges.
0.4. State the Comparison Test for a positive-termed series Pan. Let N0∈N(e.g., N0might be 17).
•If 0≤an≤cn
(only an≤cnis also ok b/c given an≥0) when n≥N0and Pcnconverges , then Panconverges.
•If 0≤dn≤an
(need 0 ≤dnpart here) when n≥N0and Pdndiverges , then Pandiverges.
Hint: sing the song to yourself.
0.5. State the Limit Comparison Test for a positive-termed series Pan.
Let bn>0 and L= limn→∞
an
bn.
•If 0 < L < ∞, then [Pbnconverges ⇐⇒ Panconverges ] .
Goal: cleverly pick positive bn’s so that you know what Pbndoes (converges or diverges) and the sequence nan
bnonconverges.
0.6. By definition, for an arbitrary series Pan, (fill in these 3 boxes with convergent or divergent).
•Panis absolutely convergent if and only if P|an|is convergent .
•Panis conditionally convergent if and only if
Panis convergent and P|an|is divergent .
•Panis divergent if and only if Panis divergent.
0.7. State the Ratio and Root Tests for arbitrary-termed series Panwith −∞ < an<∞.
Let
ρ= lim
n→∞
an+1
an
or ρ= lim
n→∞ |an|1
n.
•If ρ < 1then Panconverges absolutely.
•If ρ > 1then Pandiverges.
•If ρ= 1 then the test is inconclusive.
0.8. State the Alternating Series Test (AST).
If (1) un>0for each n∈N(2) limn→∞ un=0(3) un>(also ok ≥)un+1 for each n∈N,
then the series P(−1)nunconverges. (also ok: P(−1)n+1unconverges or P(−1)n−1unconverges)
Page 2 of 11

Spring 2016 Exam 2
1. Circle T if the statement is TRUE. Circle F if the statement if FALSE. To be more specific: circle T
if the statement is always true and circle F if the statement is NOT always true. Scoring: 2 pts for correct answer,
0 pts for an incorrect answer, 1 pt for a blank answer (indicated by a circled B).
On the next 3, think of the nth-term test for divergence and what if an=1
n
T
F B If limn→∞ an6= 0, then Pandiverges.
T
F B If Panconverges, then limn→∞ an= 0.
TF
B If limn→∞ an= 0, then Panconverges.
On the next 5, think of AC vs. CC vs. Divergent. Examples from Problem 2 might be helpful.
T
F B A series Panis precisely one of the following:
absolutely convergent, conditionally convergent, divergent.
T
F B If an≥0 for all n∈N, then Panis either absolutely convergent or divergent.
T
F B If P|an|converges, then Panconverges.
T
F B If Pandiverges, then P|an|diverges.
TF
B If P|an|diverges, then Pandiverges.
On the next 2, think of a Theorem from class and what if bn=−an.
T
F B If Panconverges and Pbnconverge, then P(an+bn) converges.
TF
B If P(an+bn) converges, then Panconverges and Pbnconverge.
2. Circle the behavior of the given series. The abbreviations are:
•AC stands for absolutely convergent
•CC stands for conditionally convergent •DVG stand for divergent
•NOT stands for none of the others.
You can circle up to 1answers for each problem. The scoring is as follows.
•For a problem with precisely one answer marked and the answer is correct, 1 points.
•All other cases, 0 points.
Series
∞
X
n=1
1
n2AC
CC DVG NOT
∞
X
n=1
(−1)n
n2AC
CC DVG NOT
∞
X
n=1
1
nAC CC DVG
NOT
∞
X
n=1
(−1)n
nAC CC
DVG NOT
∞
X
n=1
1
√nAC CC DVG
NOT
∞
X
n=1
(−1)n
√nAC CC
DVG NOT
∞
X
n=2
1
ln(n)AC CC DVG
NOT
∞
X
n=2
(−1)n
ln(n)AC CC
DVG NOT
∞
X
n=1
1
enAC
CC DVG NOT
∞
X
n=1
(−1)n
enAC
CC DVG NOT
Page 3 of 11
Document Summary
0, then your score for the entire exam will be whatever you made on problem 0: on problem 0, ll in the blanks. As you know, if you do not make at least half of the points on problem: for multiple choice problems, circle your answer(s) on the provided chart. Unauthorized materials include: elec- tronic devices, books, and personal notes. This means no electronic devices (such as cell phones) allowed in your pockets. At a students request, i will project my watch upon the projector screen. hand. When you nish: put your pencil down and raise your hand: during this exam, do not leave your seat unless you have permission. If you have a question, raise your: this exam covers (from calculus by thomas, 13th ed. , et): 10. 1 10. 6 . I understand that it is the responsibility of every member of the carolina community to uphold and maintain the university of south carolina"s honor code.