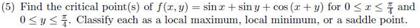MATH 0240 Midterm: MATH 240 Midterm 2-65
Document Summary
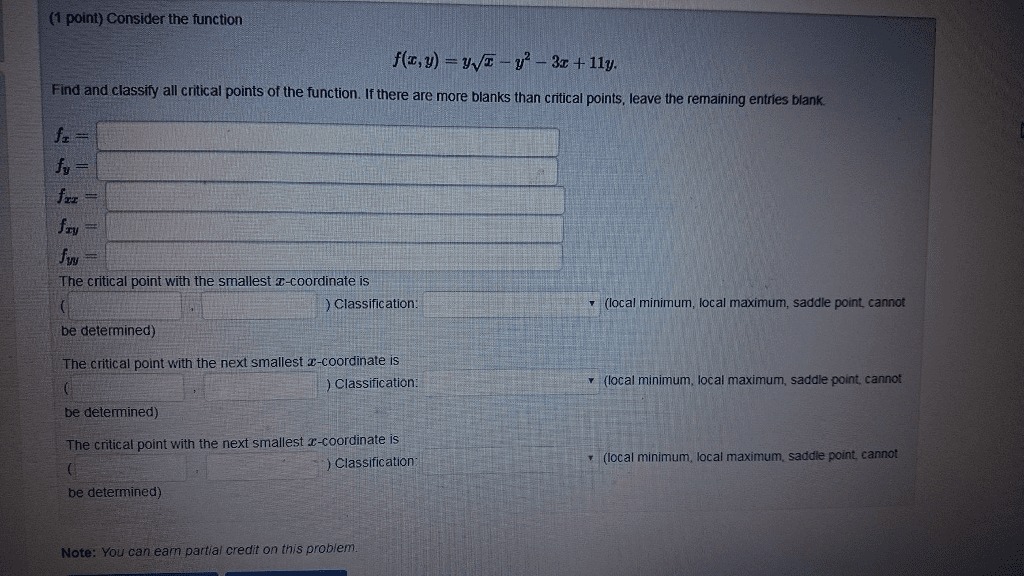
All work must be shown in order to get credit. Please write legibly and explain your logic by words whenever appropriate. If more space is needed, write on the back of the pages and/or ask for more paper. Problem 1. a) find all critical points of f (x, y) = x2y3 + xy2 + 2xy: for each critical point, classify the point as a local maximum, a local minimum, or a saddle point. Find the absolute maximum value of the function f (x, y) = x2 y on the circle x2 + y2 = 25. Find the center of mass of the lamina that has a constant density and occupies the region d, bounded by the curves x = 1 y2 and y = x + 1. Find the shortest distance from the surface xyz = 1 to the origin.