MATH 0240 Final: MATH 240 Final Exam-49
Document Summary
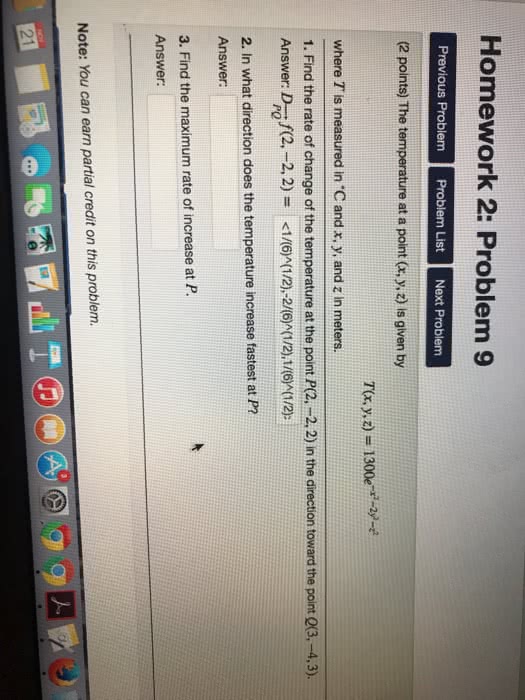
Find the minimum distance between the lines (x, y, z) = t(1, 1, 1), t r, and (x, y, z) = ( 1, 2, 1) + s(1, 0, 1), s r. Determine all points at which function f (x, y) = xy attains its absolute minima and maxima on the region. D = {(x, y) : x 0, y 0, and y 1 x2}. Let f (x, y, z) = x + y2 + z3, de ned on r3, and let. P = (0, 1, 1): compute the gradient of f at point p, at point p nd the direction along which f shows maximal decrease, find the directional derivative of f at point p in the direction of. < 1, 0, 2 > . at point p: write the equation of the line normal to the surface x + y2 + z3 2 = 0.