MATH 222 Midterm: MATH 222 KSU Test 1s01
15 Feb 2019
School
Department
Course
Professor
Document Summary
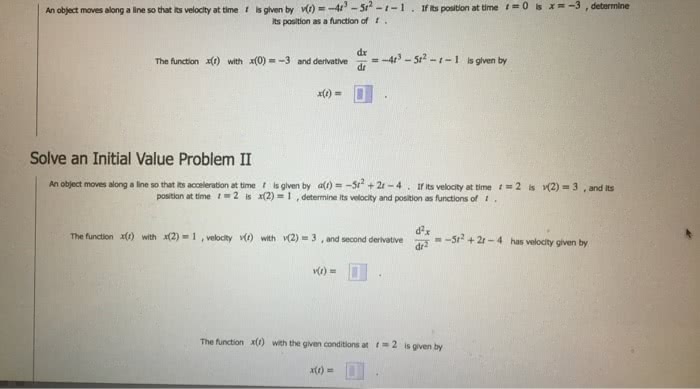
To receive credit you must show your work. (25) 1. An object is moving in the plane according to the parametric equations t2, y = t3 where t is the time. An object is moving in 3-space in such a way that its acceleration vector as a function of time is ~a = ~j + (cos t)~k. An object is moving in the plane along the curve y = right. It is moving at a constant speed of 3 ft/sec: find at and an when the object is at (cid:18)x, 2 x2, from left to: find the velocity vector and the acceleration vector when the object is at the point (cid:18)1, Given the vectors ~a = ~i + ~j ~k, ~b = ~i + 2~j + 5~k, ~c = ~i + ~k: calculate the volume of the parallelepiped which is determined by the vectors.
