MATH 222 Midterm: MATH 222 KSU Test 3f97

• School: Kansas State University
• Department: Mathematics
• Course: MATH 222
• Professor: All

Document Summary

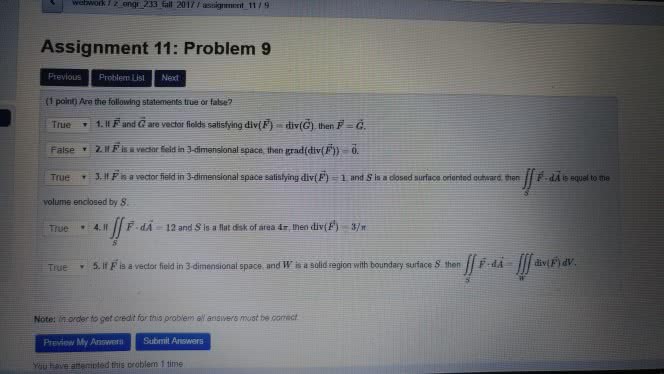
To receive credit you must show your work. (10) 1. Find the volume of the 3-dimensional region which is under the surface z = 1 + xy and above the rectangle 0 x 2 , 0 y 3 in the xy plane. Find the volume of the 3-dimensional region which is enclosed by the surfaces y = x2 , y = 2x , z = y and z = 6 . 2x cos(y2)dy dx by rst reversing the order of. A mass distribution occupies the region which is enclosed by the surfaces z = 2 x2 y2 and z = x2 + y2 . (x, y, z) = 2z units of mass/unit volume. A mass distribution occupies the region which is above the surface z = px2 + y2 and under the plane z = 2 . The mass density function is (x, y, z) = zpx2 + y2 + z2 units of mass/unit volume.