MAC-2311 Midterm: MAC 2311-17 test-4-key
Document Summary
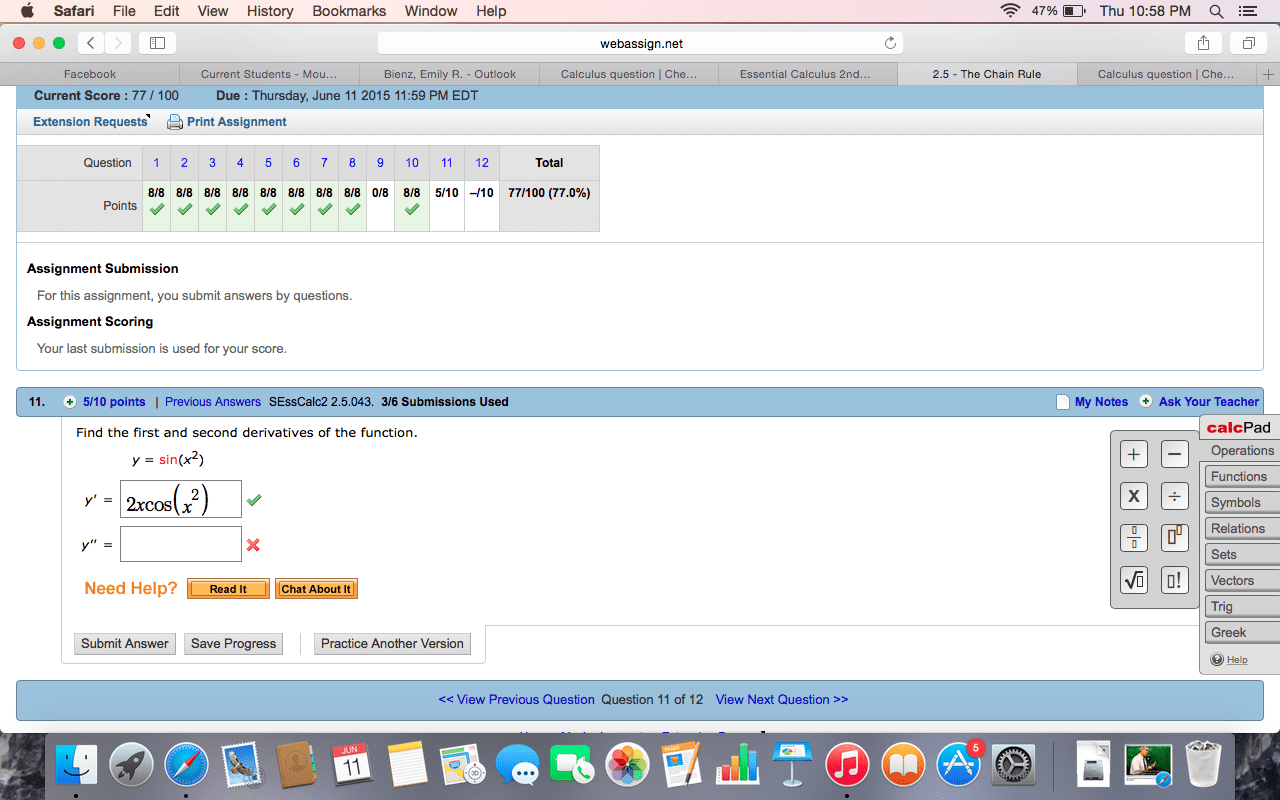
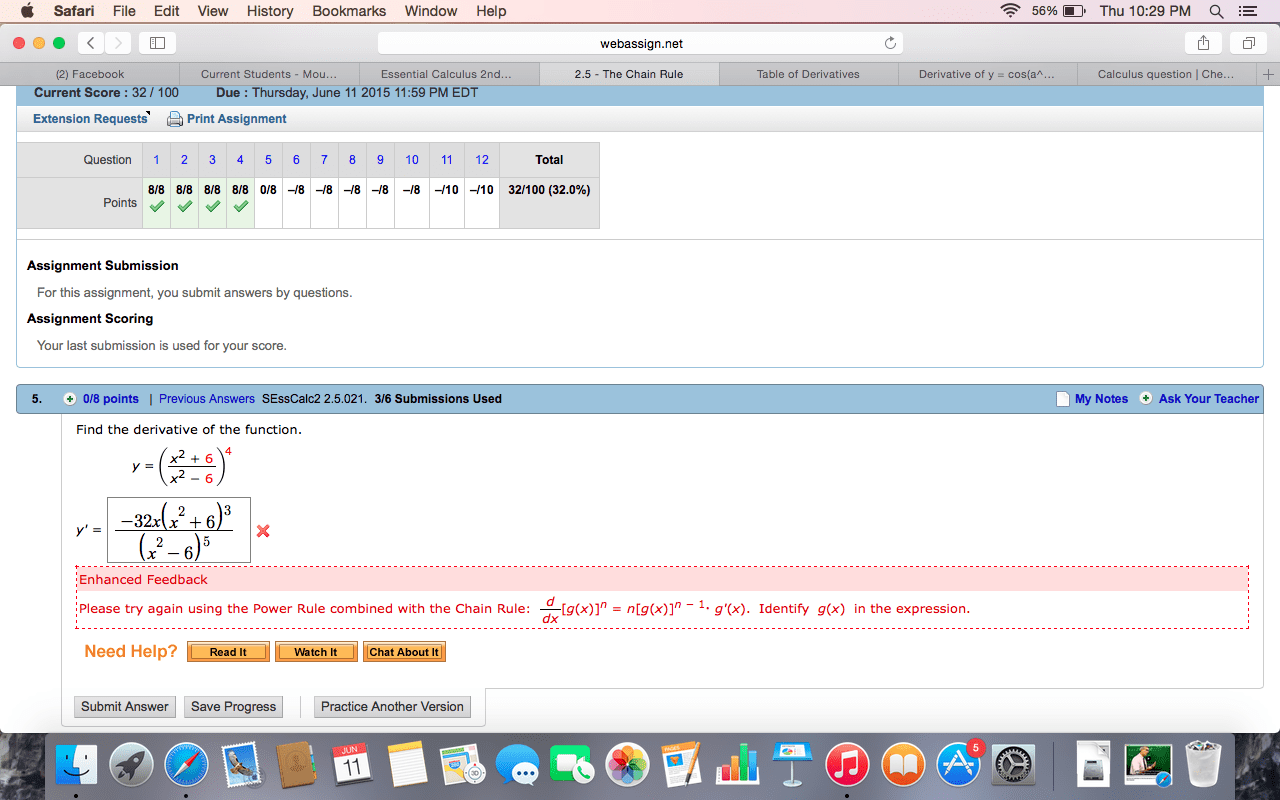
You may use the back of a page if you need more space for a problem. Solution: solving the linearization given for xn+1, we have newton"s formula: xn+1 = xn f (xn) f (xn) . We are trying to approximate the solution of the equation x = cos(x) that is near x = /4. So, f (x) = x cos(x) and f (x) = 1 sin(x). Starting from x1 = /4, we get x2 = x1 f (x1) f (x1) 1 1/ 2: in each part, nd the inde nite integral or de nite integral given if it exists. If it does not exist, explain why. (a) (6 points) z (cid:0)3x2 + x + ex(cid:1) dx. Z (cid:0)3x2 + x + ex(cid:1) dx = z (cid:0)3x2 + x1/2 + ex(cid:1) dx. 3 x3/2 + ex + c. (b) (6 points) z 2x3 3 x. 2x dx = z (x2 x 1/2) dx.