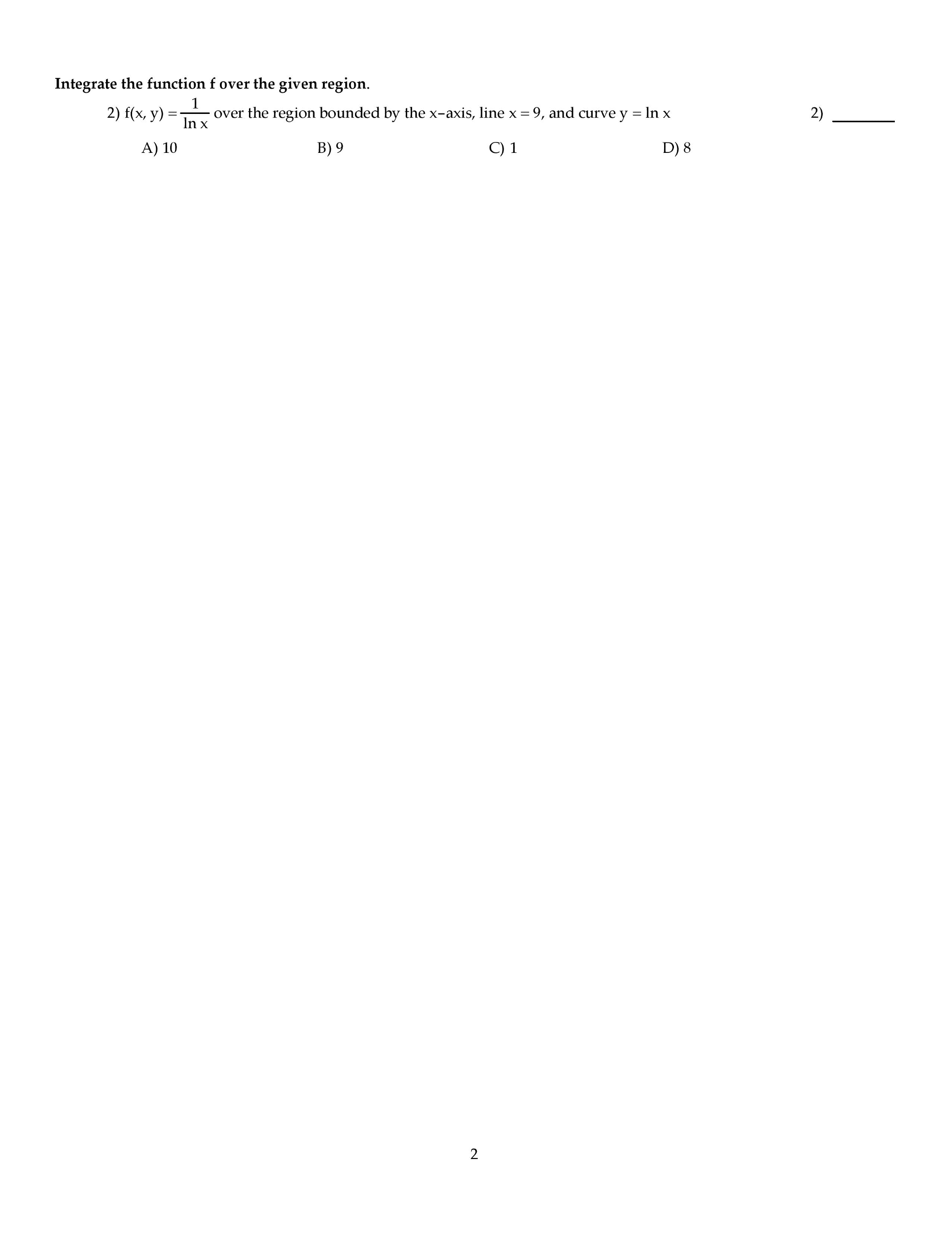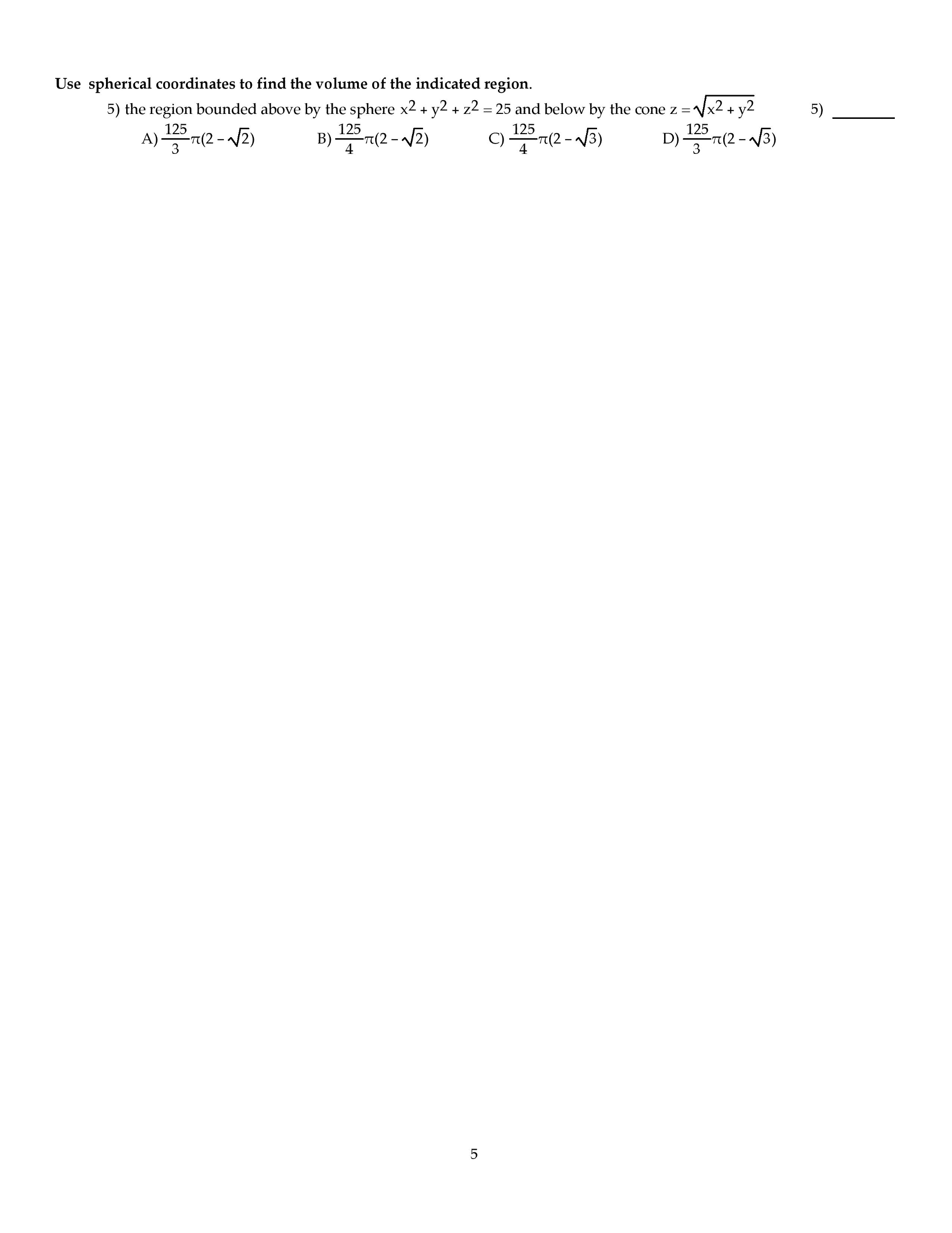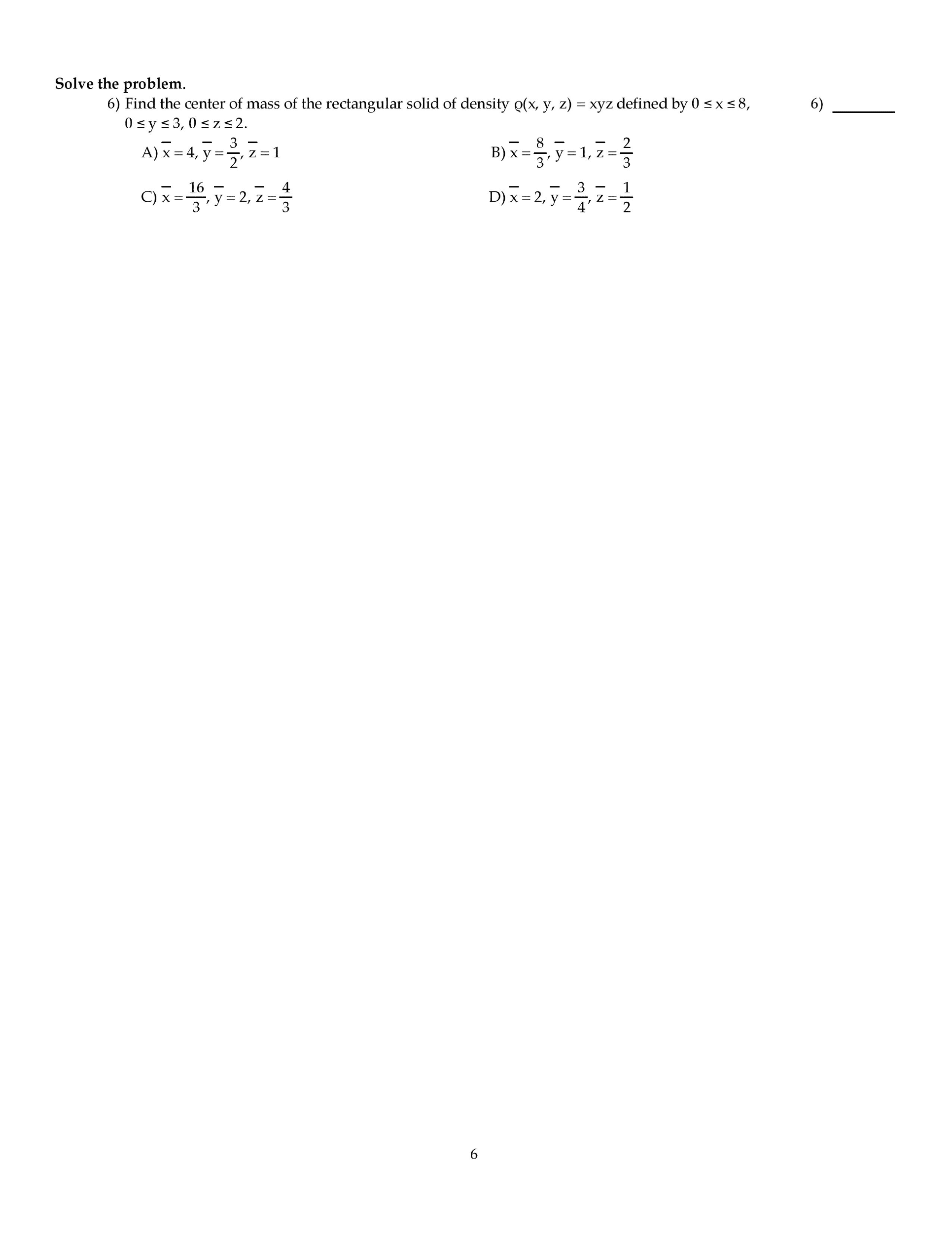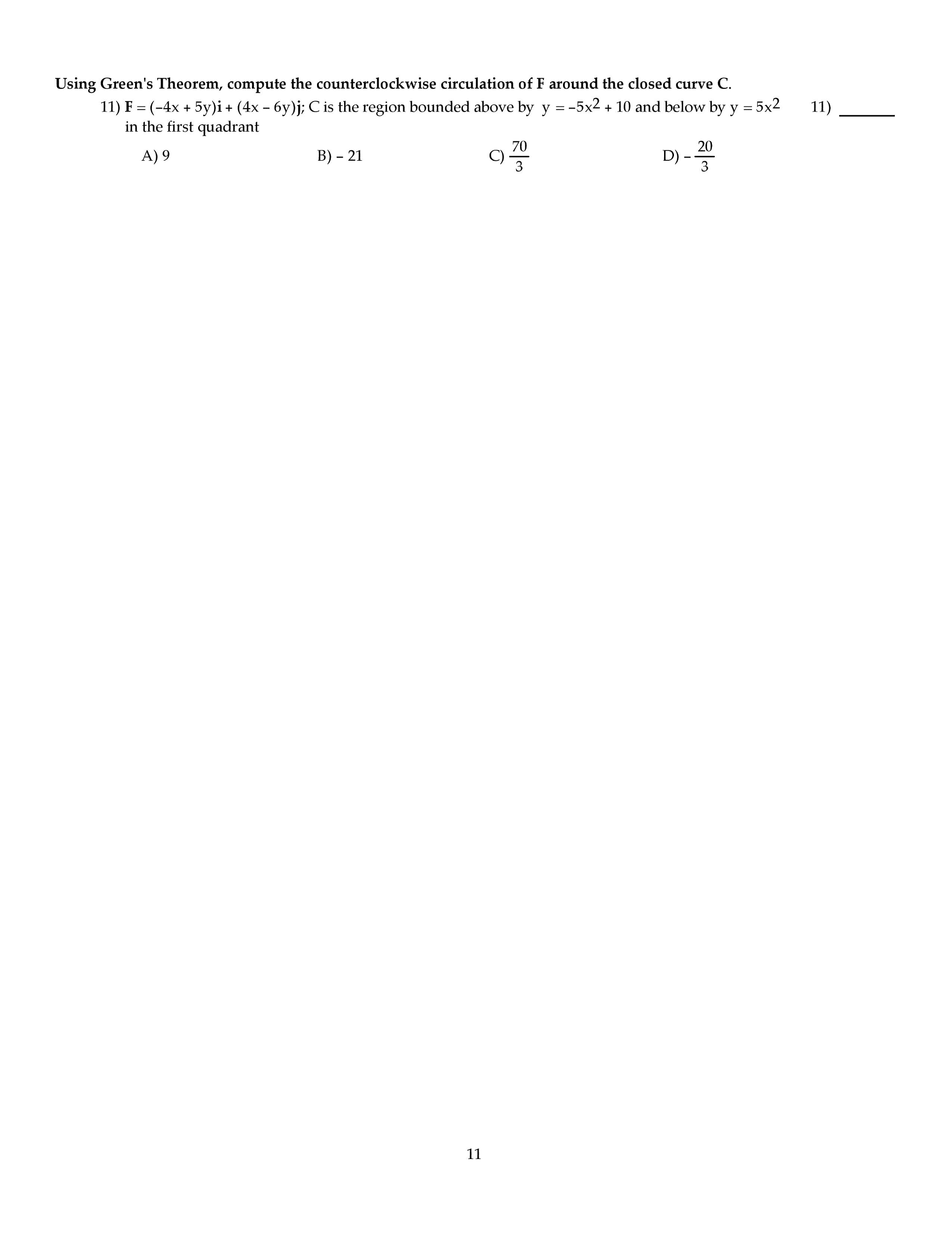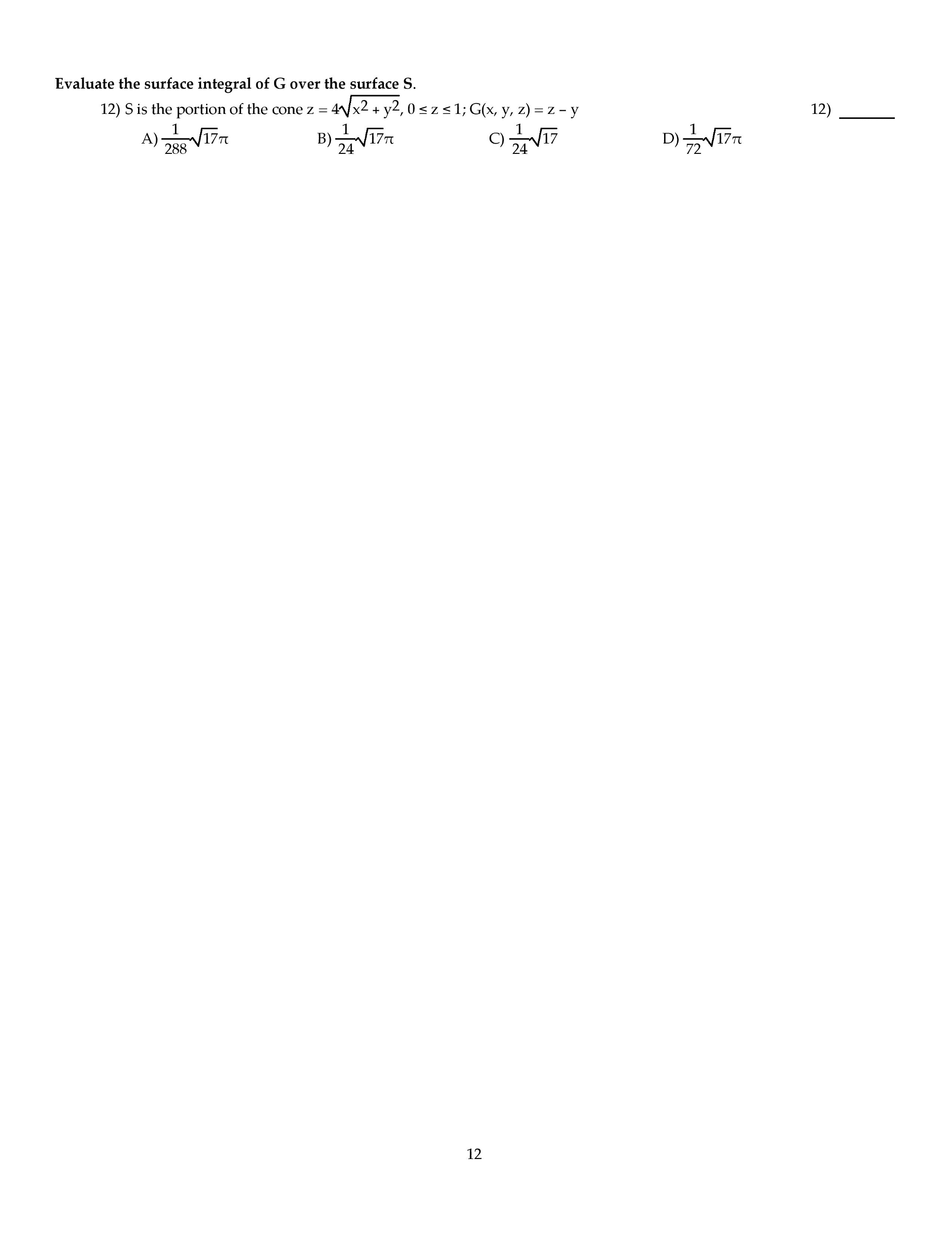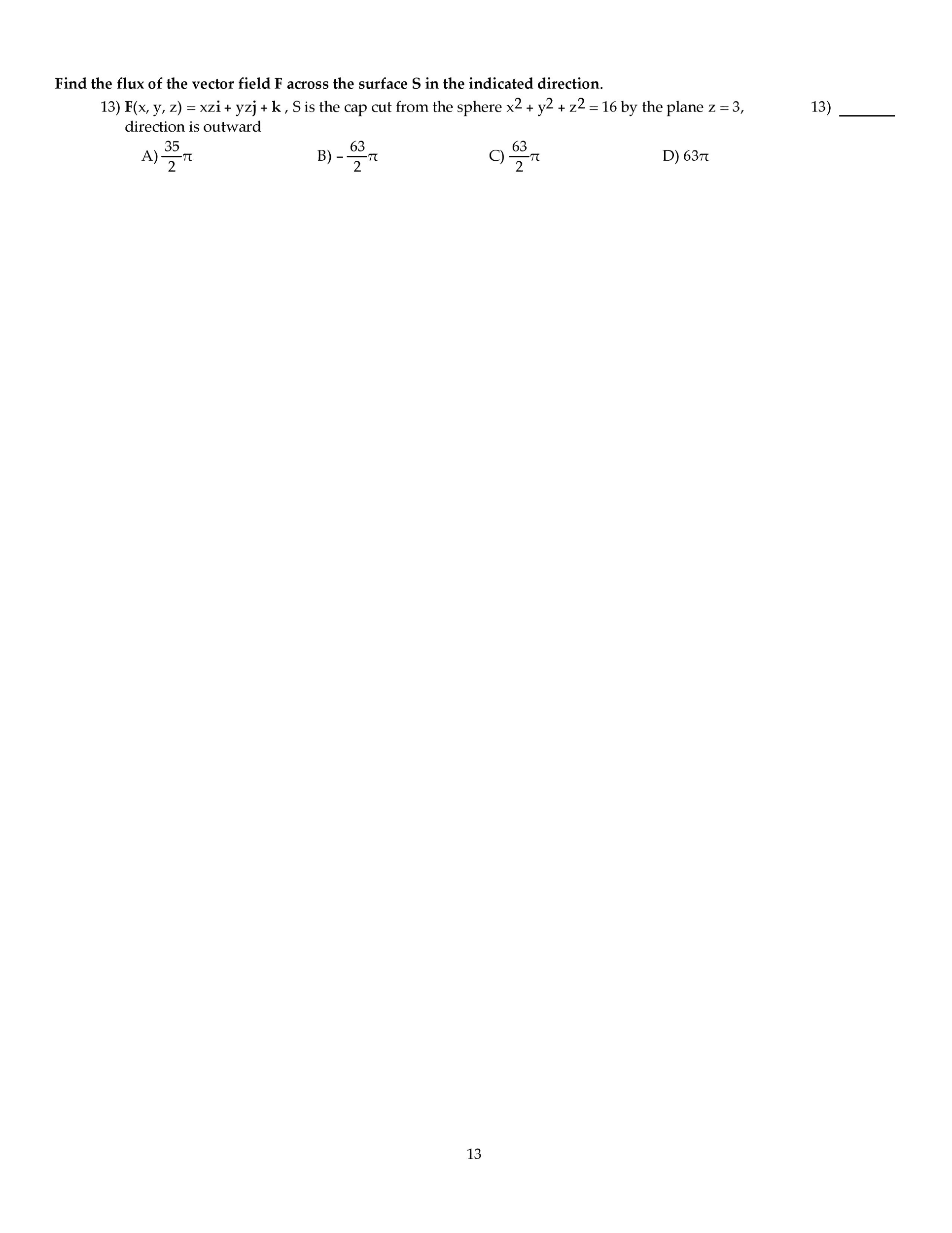MAC 2311 Midterm: MAC 2311 FIU Exam 307k
15 Feb 2019
School
Department
Course
Professor
MAC 2311 April 5, 2007
Exam III and Key Prof. S. Hudson.
1) (10pts) A spherical balloon is inflated so that its volume (V= 4πr3/3) is increasing at
a rate of 3 ft3/min. How fast is the diameter increasing when the radius is 1 ft.?
2) (10pts) Compute each limit (and show work);
a) limx→+∞(1 −2/x)x
b) limx→0tan(x)
tan−1(x)
3) (25pts) Compute:
a) Find dy/dx:y=e1/x
b) Find dy/dx:y= tan−1(x3)
c) Find dy/dx using logarithmic differentiation: y=xx
d) Find dy/dx using implicit differentiation: x2+y2= 100
e) Find d2y/dx2using implicit differentiation: 2x2−3y2= 4
4) (15 pts) Give an example of a function f(x) for each part, or explain why none exists.
[Give three separate answers].
a) It has a stationary point at x= 0, but that point is not a relative extrema.
b) It has a relative extrema at x= 0, but that point is not a stationary point.
c) f′′(0) = 0 but x= 0 is not an inflection point.
5) (10pts) Prove that d
dx sin−1(x) = 1
√1−x2using a theorem about inverse functions (or
the chain rule).
6) (10pts) Answer True or False:
tan−1(x) has a maximum value on (−∞,+∞).
Every quadratic polynomial has exactly one critical point.
If f′(x)<0 on (a,b), then fis decreasing on (a,b).
If fhas only one relative extrema on I, and it is a relative minima, then it is also an
absolute minima.
If fis continuous on (a,b) and lim f=−∞ as x→a+and as x→b−then fhas an
absolute max but no absolute min on (a,b).
1
Document Summary
Prof. s. hudson: (10pts) a spherical balloon is in ated so that its volume (v = 4 r3/3) is increasing at a rate of 3 ft3/min. 1 x2 using a theorem about inverse functions (or: (10pts) answer true or false: tan 1(x) has a maximum value on ( , + ). Every quadratic polynomial has exactly one critical point. If f (x) < 0 on (a,b), then f is decreasing on (a,b). If f has only one relative extrema on i, and it is a relative minima, then it is also an absolute minima. If f is continuous on (a,b) and lim f = as x a+ and as x b then f has an absolute max but no absolute min on (a,b). 1: (10pts) sketch a graph of f (x) = 1/(x2 1) paying special attention to any asymptotes and critical points.
