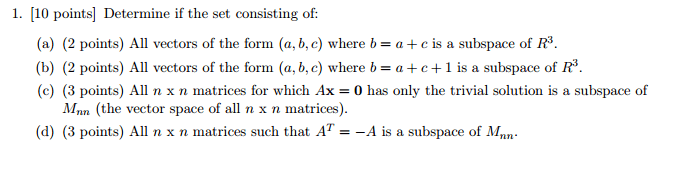MATH 3001 Final: exam2_review1_problems
Document Summary
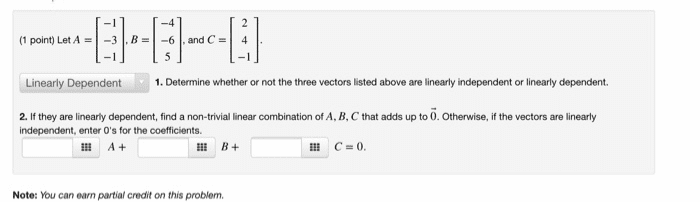
Linear independence of vectors: determine if the following collection of vectors in r3 are linearly inde- pendent. If the vectors are linearly dependent, nd a basis for the set of vectors (a) (b) . Linear independence of functions: determine if the following functions are linearly independent. (a) p1(t) = t + 1, p2(t) = t 1, p3(t) = 1 + t + t2. (b) (cid:8)cos2(x), sin2(x), 1(cid:9). Spaces derived from matrices: let a be given by a = . Vector subspaces: determine whether or not the space of all symmetric matrices form a vector subspace in the vector space of all matrices. Matrix equations: solve a~x = ~b where (a) a = .