HomeStudy Guides420,000US230,000

APPM 2360 Midterm: appm2360summer2014exam3_sol

20 views4 pages

turquoisegnu128

31 Jan 2019

School

Department

Course

Professor

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

On the front of your bluebook write: (1) your name, (2) your student id number, (3) your instructor"s name, and (4) a grading table. Text books, class notes, and calculators are not permitted. Problem 1: (25 points) consider the ode t2y + ty 4y = f (t). (a) let f (t) = 0. Explain your response. (c) find a particular solution to the ode for f (t) = 4t 4. (d) find the general solution to the ode for f (t) = 4t 4. The ode yields the equation tr(r(r 1) + r 4) = 0. So we solve r2 4 = 0 to get r = 2 . (b) s = {t2, t 2} forms the basis for the solution space of this ode . Note that this vector space must have dimension two because the ode is second order. We claim that s is a linearly independent set via the wronskian: t2.

Related textbook solutions

Calculus

ISBN: 9781319050733

Single Variable Calculus: Early Transcendentals

4th Edition, 2018

ISBN: 9781337687805

CALCULUS:EARLY TRANSCENDENTALS

ISBN: 9781319050740

Related Documents

APPM 2360 Midterm: appm2360summer2014exam3

turquoisegnu128

APPM 2360 Midterm: archive_appm2360fall2018exam3

turquoisegnu128

APPM 2360 Midterm: appm2360summer2015exam11_sol

turquoisegnu128

Related Questions

Algebra

Complete the sentence below. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. Complete the sentence below. The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and If r is a solution to the equation f(x) = 05 name three additional statements that can be made about f and r assuming f is a polynomial function. Choose the correct answer below. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is an x-intercept of the graph of and x - r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a complex zero of the polynomial function r is an x-intercept of the graph of and x + r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is a y-intercept of the graph of x and x + r is a factor of f. Explain what the notation Km f(x) = -infinity means. x rightarrow infinity Choose the correct answer below. The limit of f(x) as x approaches - infinity equals infinity. The limit of x as f(x) approaches infinity equals - infinity. The limit of f(x) as x approaches infinity equals - infinity. The limit of x as f(x) approaches - infinity equals infinity. Form a polynomial whose zeros and degree are given. Zeros: -7, multiplicity 1; - 3, multiplicity 2; degree 3 Type a polynomial with integer coefficients and a leading coefficient of 1 in the box below. F(x) = Find the vertical horizontal and oblique asymptotes, if any, for the following rational function.R(x) = 12x / x + 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, of the given rational function. R(x) = x3 - 64 / x2 - 6x + 8 Find the vertical asymptote(s), if any, of the function. Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Simplify your answer. Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, for the given rational function. Q(x) = 2x2 - 7x - 4 / 3x2 - 7x - 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed. Use integers or fractions for any numbers in the expression.) There is no vertical asymptote. Analyze the graph of the function. R(x) = x + 14 / x(x + 15) What is the domain of R(x)? {x x 0 andx - 16} {x x 0 andx - 16 andx - 14} {x x 0 and x - 14} All real numbers Analyze the graph of the function. R(x) = 5x + 5 / 4x + 12 What is the domain of R(x)? {x|x 0 and x -3 and x - 1} {x|x -3} {x|x and x - 3} All real numbers Analyze the graph of the function.R(x) = x2 / x2 + x - 56 What is the domain of R(x)? {x|x 7 and x - 8} {x|x 0,x -1, and x 8} {x|x 0, x 7, and x - 8} All real numbers

Show transcribed image text Complete the sentence below. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. Complete the sentence below. The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and If r is a solution to the equation f(x) = 05 name three additional statements that can be made about f and r assuming f is a polynomial function. Choose the correct answer below. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is an x-intercept of the graph of and x - r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a complex zero of the polynomial function r is an x-intercept of the graph of and x + r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is a y-intercept of the graph of x and x + r is a factor of f. Explain what the notation Km f(x) = -infinity means. x rightarrow infinity Choose the correct answer below. The limit of f(x) as x approaches - infinity equals infinity. The limit of x as f(x) approaches infinity equals - infinity. The limit of f(x) as x approaches infinity equals - infinity. The limit of x as f(x) approaches - infinity equals infinity. Form a polynomial whose zeros and degree are given. Zeros: -7, multiplicity 1; - 3, multiplicity 2; degree 3 Type a polynomial with integer coefficients and a leading coefficient of 1 in the box below. F(x) = Find the vertical horizontal and oblique asymptotes, if any, for the following rational function.R(x) = 12x / x + 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, of the given rational function. R(x) = x3 - 64 / x2 - 6x + 8 Find the vertical asymptote(s), if any, of the function. Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Simplify your answer. Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, for the given rational function. Q(x) = 2x2 - 7x - 4 / 3x2 - 7x - 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed. Use integers or fractions for any numbers in the expression.) There is no vertical asymptote. Analyze the graph of the function. R(x) = x + 14 / x(x + 15) What is the domain of R(x)? {x x 0 andx - 16} {x x 0 andx - 16 andx - 14} {x x 0 and x - 14} All real numbers Analyze the graph of the function. R(x) = 5x + 5 / 4x + 12 What is the domain of R(x)? {x|x 0 and x -3 and x - 1} {x|x -3} {x|x and x - 3} All real numbers Analyze the graph of the function.R(x) = x2 / x2 + x - 56 What is the domain of R(x)? {x|x 7 and x - 8} {x|x 0,x -1, and x 8} {x|x 0, x 7, and x - 8} All real numbers

indigosardine988

Solve all please.

INSTRUCTIONS: There are 15 problems on this exam, and each problem is worth 13 points, plus 5 points for writing down an approximate volume of the planet Earth in cubic miles at the bottomleft corner of page 3, for a total possible 200 points. For this exam, you are allowed to use one 8.5"X11" sheet of notes (both sides, in your own handwriting), pencil, eraser, ruler, scratch paper and calculator. Even though the questions are multiple-choice, you need to show enough work to justify your answer in order to receive full credit. After you have determined the correct solution to each problem, write the letter corresponding to your answer in the appropriate space on the right side of the page AND circle your answer. If your answer does not agree with any of the choices, after double-checking your work, choose option E) and prominently mark your answer (box, circle, underline, etc.). Time limit: Two hours. Attach (i.e. staple) any notecard and scratch paper to the rear of this exam paper. Good luck! MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. The northern third of Indiana is a rectangle measuring 96 miles by 132 miles. Thus, let D = [0, 96] times [0,132]. Assuming that the total annual snowfall (in inches), S(x,y), at (x,y) euro D is given by the function S(x,y) = 60e-0.001 (2x + y) with (x,y) euro D, find the average snowfall on D. 51.14 inches 52.06 inches 51.78 inches 52.44 inches Evaluate the work done between point 1 and point 2 for the conservative field F. Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C. Evaluate the surface integral of G over the surface S. S is the portion of the cone Find the flux of the vector field F across the surface S in the indicated direction. Using the Divergence Theorem, find the outward flux of F across the boundary of the region D. Integrate the function f over the given region. f(x,y) = 1/ln x over the region bounded by the x-axis, line x = 9, and curvey y = ln x Reverse the order of integration and then evaluate the integral Use a double integral in polar coordinates to find the area of the region specified in polar coordinates. the region inside both r = 7 sin Theta and r = 7 cos Theta Use spherical coordinates to find the volume of the indicated region. the region bounded above by the sphere x2 + y2 + z2 = 25 and below by the cone z = Find the center of mass of the rectangular solid of density (x,y,z) = xyz defined by 0 LE x LE 8, Use the given transformation to evaluate the integral. where R is the parallelogram bounded by the lines y = 8x + 8, y = 8x +9, y = -6x + 2, y = -6x +7 Evaluate the line integral along the curve C. Find the work done by F over the curve in the direction of increasing t.

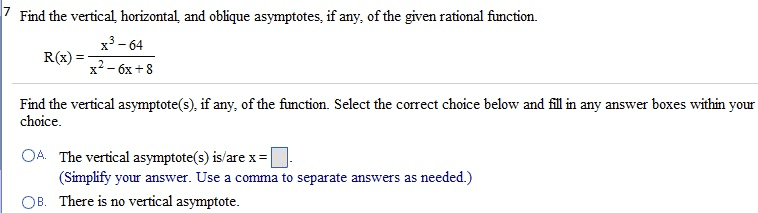
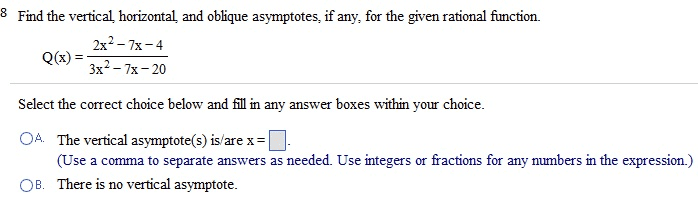
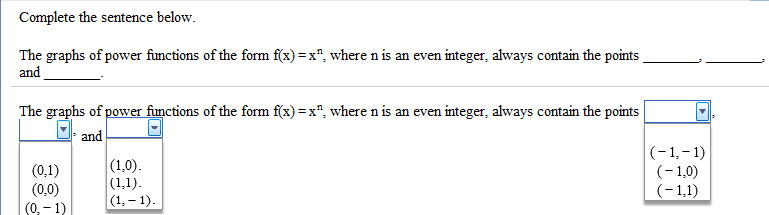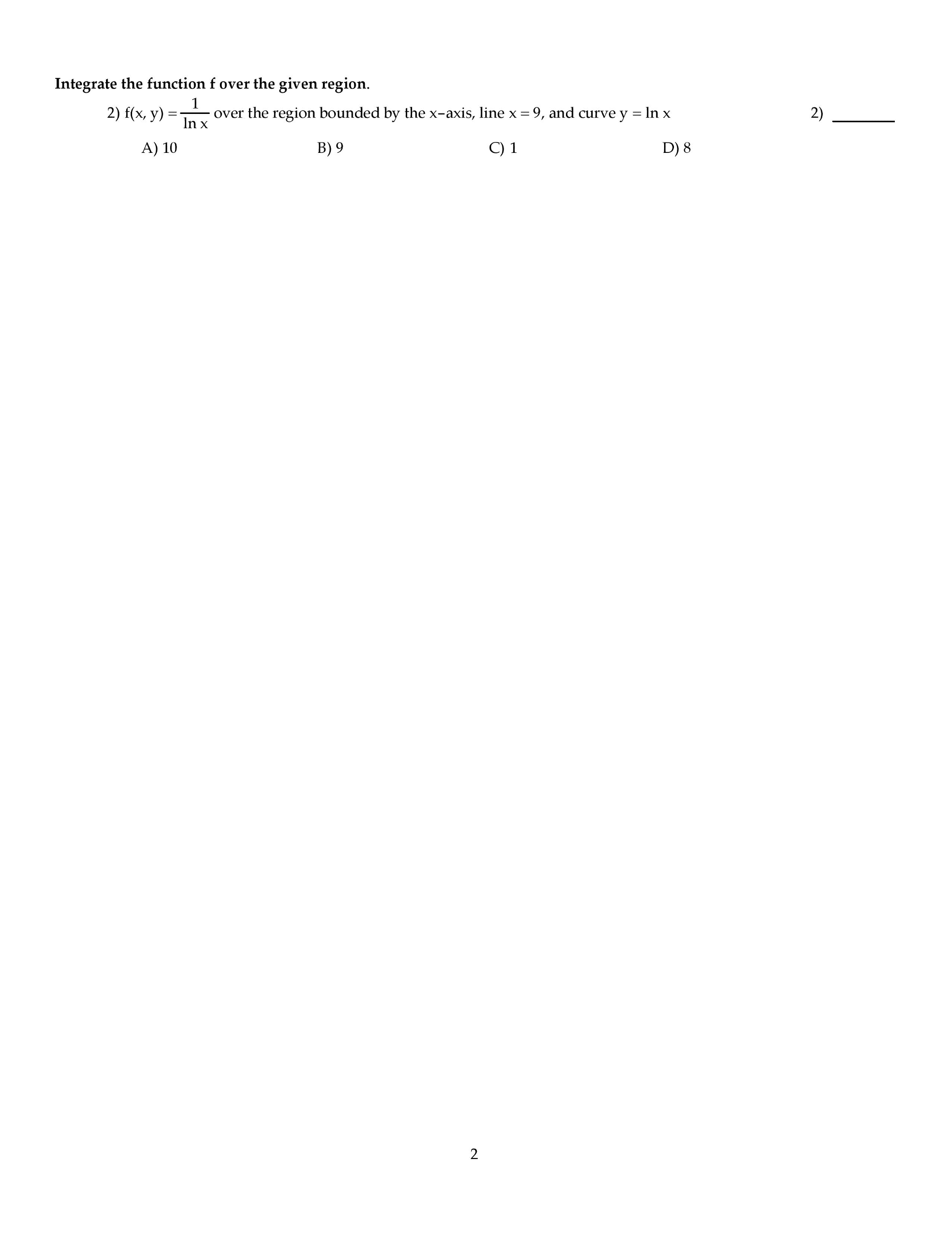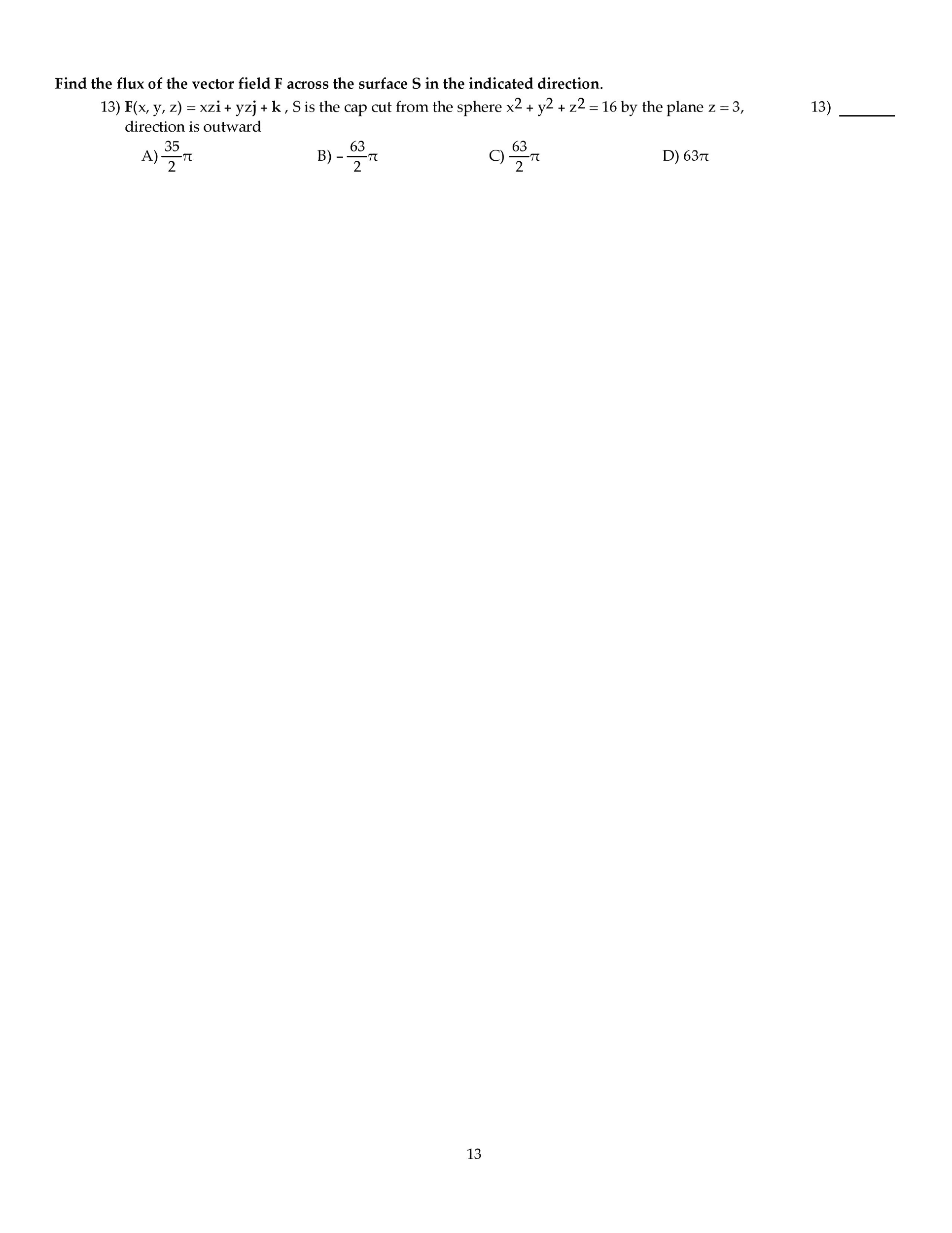Thank you in advance..

Show transcribed image text Homework: Homework 7 Score: 0 of 1 pt 17.7.18 Save 1 of 15 (10 complete) HW Score: 55.56%, 8.33 of 15 pts Question Help r a particular product is N x y -6 xo y 4 where o produce N x y un s o he product Each unit t labor costs $40 and each unit ot he Cobb Do las production unction s the number o units o labor and y s he number o units cap a equire capital costs $100 t Sba i duchon ot the product, determine how that amount should be allocated to maximize production Production will be maximiced whhen usurils of labor adurisof capilal s budgeted tor pro
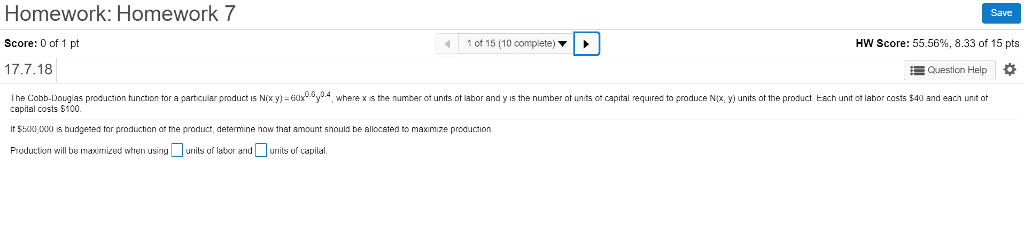
Homework: Homework 7 Save Score: 0 of 1 pt 42 of 15 (10 complete) HW Score: 55.56%, 8.33 of 1 5 pts 14.8.3 Find the maximum value of txy)-23-x2 -y on the line x+4y 17 Tne maximum value of t(x y)-23-x2-y2 on the line x 1 4y-171sN. Question Help (Simplify your answer)
Homework: Homework 7 Save Score: 0 of 1 pt 3 of 15 (10 complete) â¼ HW Score: 55.56%, 8.33 of 15 pts *14.8.26 Question Heip Findthe lagest product the positive nurmbers x, y, ard z can have if xy2-9 The product is Type an exact answer, using redicals as needed.)
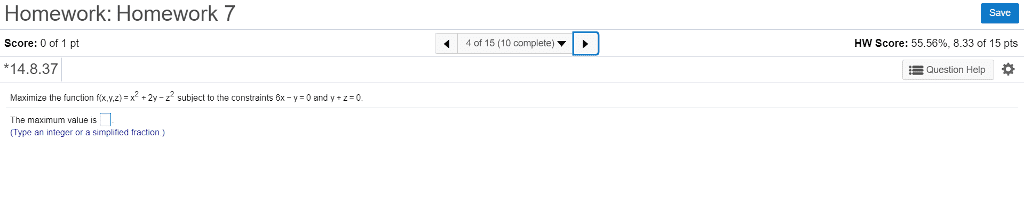
Homework: Homework 7 Save Score: 0 of 1 pt 4 of 15 (10 complete- HW Score: 55.56%, 8.33 of 15 pts 14.8.37 Quesion Help Maximize the function f(x.wz,-x2Â·2y-z2 subiect to the constraints 6x-y-oond y.z-o Ihe maxmum value is (Type an integer or a simplifed traction ã
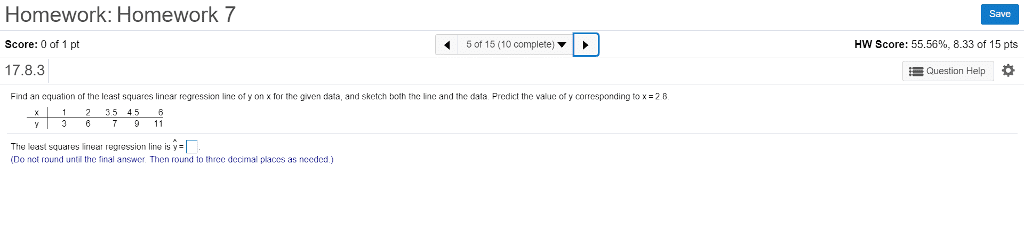
Homework: Homework7 Score: 0 of 1 pt 17.8.3 Find an equation of the least squares lincar regression line ofy on x for the given data, and sketch both the lne and the data Predict the value ofy corresponding to x2B Save 5 of 15 (10 complete) HW Score: 55.56%, 8.33 of 15 pts Question Help x1235 45 6 36911 The least squares inear regression line is y- Do not round unti the final answer Then round to three decimal placos as nceded)
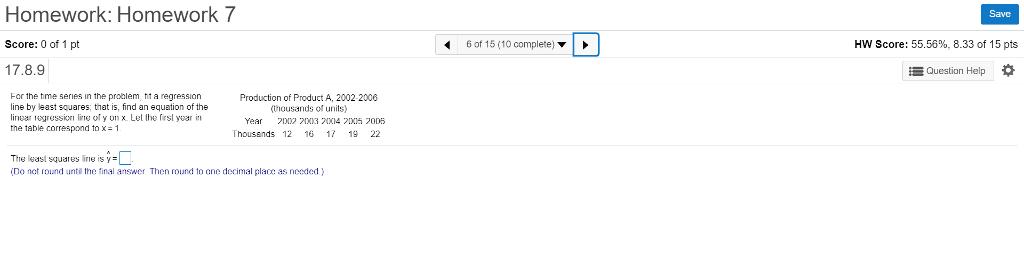
Save Homework: Homework Score: 0 of 1 pt 17.8.9 6 of 15 (10 complete) HW Score: 55.56%, 8.33 of 15 pts Question Help For the tme series in the problem, a regressian line by least squares, that is, find an equation of the linear eressicrn l ofynx. Lel lhe firsl year in the table correspond to x= 1 Production of Product A, 2002-2006 thousands of unils) Year XI4 20DS Thousands 12 16 17 19 22 The least squares ine is y= (Do not round unti the final answer Then round to one decimal place as needed ã

lemonantelope692