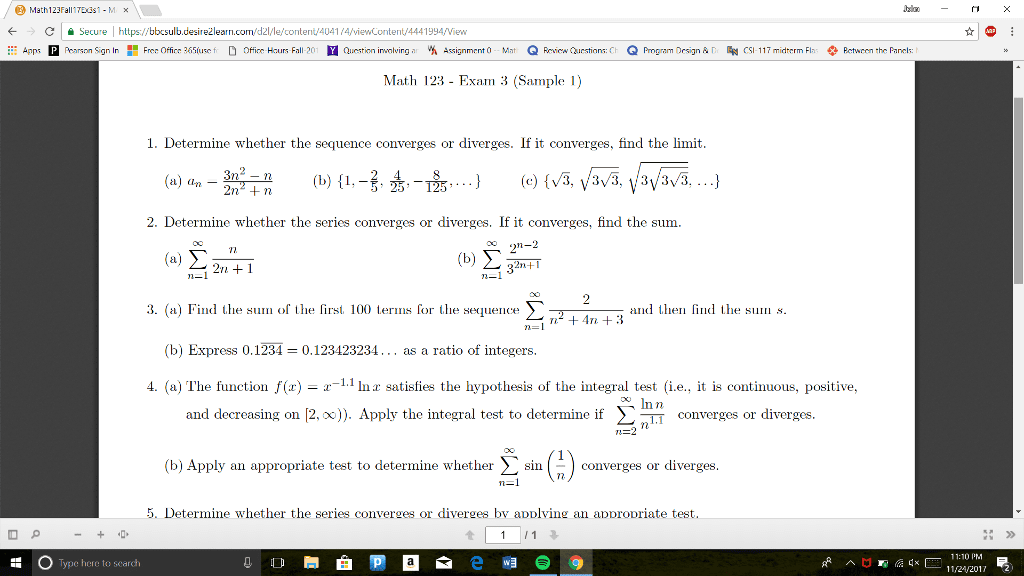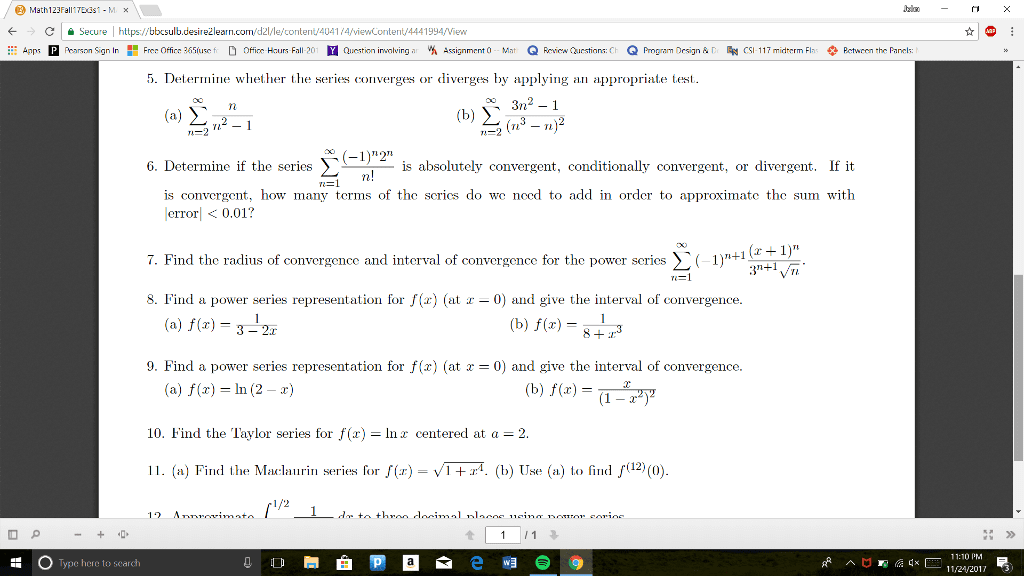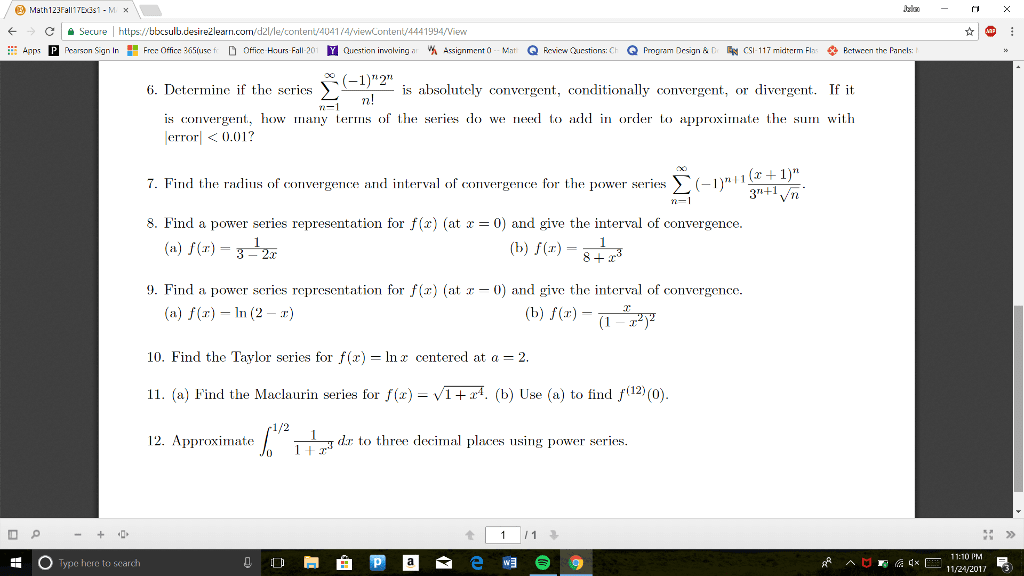APPM 1360 Midterm: archive_appm1360fall2018exam3_sol
Document Summary
Fall 2018: [36 pts] determine if the following series converge absolutely, converge conditionally or diverge. Be sure to fully justify your answer and state any test you use. (a) e3n nn. Series converges absolutely by the root test. lim n e3 n. = 0 < 1 ns(cid:12)(cid:12)(cid:12)(cid:12) e3n nn (cid:12)(cid:12)(cid:12)(cid:12) (b) each term of the series is positive and as n gets large, the terms begin to look like 28n2/4n7/2 = 7n 3/2. 28 + 5 n2 q16 + 3 n5 + 2 n7. 1 n3/2 is a p series with p = 3/2 > 1 it converges, and the original series converges by the limit. Since all of the terms of the series are positive, the series converges absolutely. (c) note that the terms of the series are an = ( 1)n and we consider lim n (cid:12)(cid:12)(cid:12)(cid:12) an+1 an (cid:12)(cid:12)(cid:12)(cid:12)