HomeStudy Guides420,000CA160,000

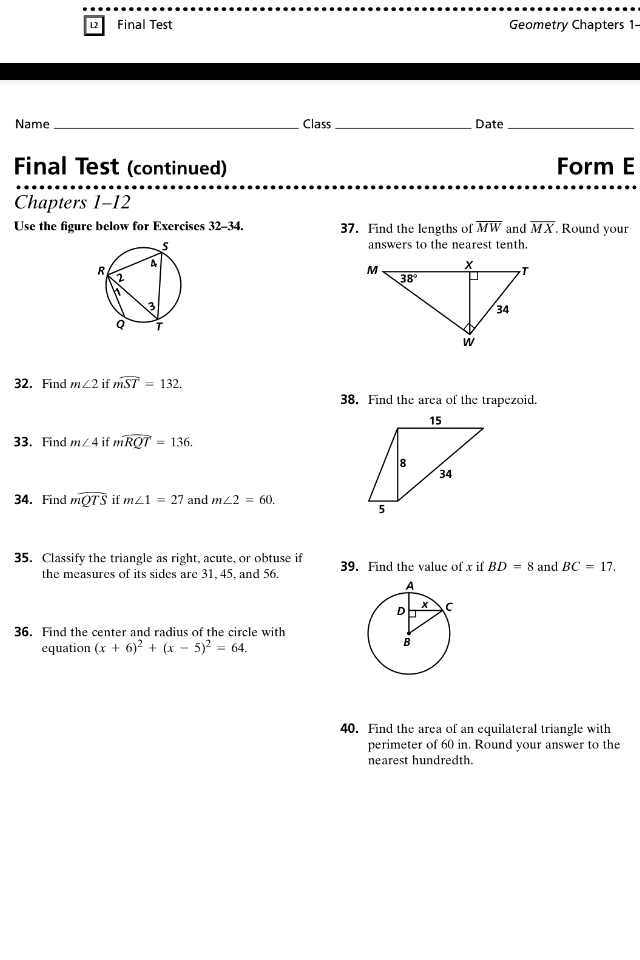
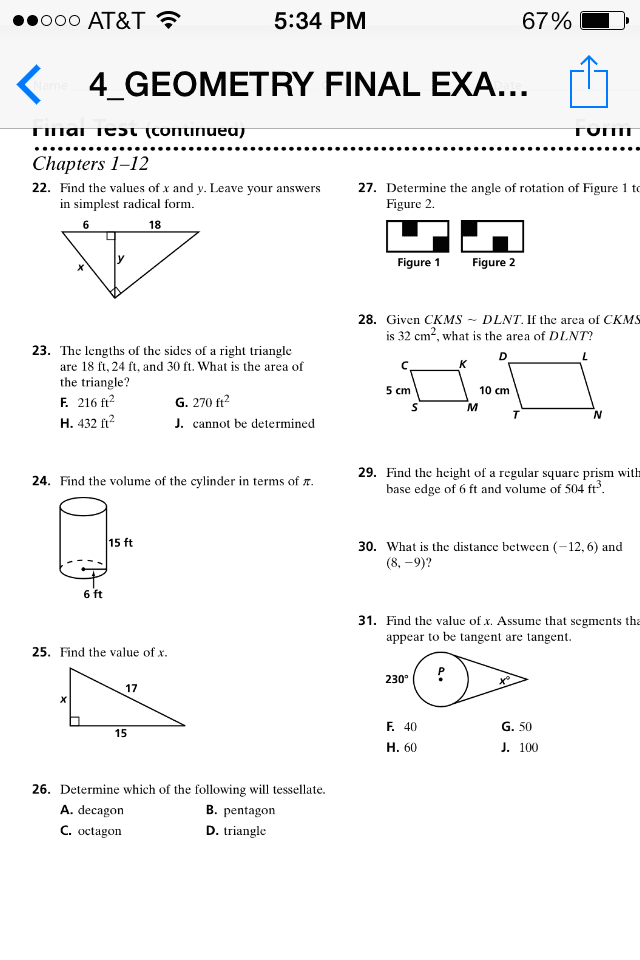
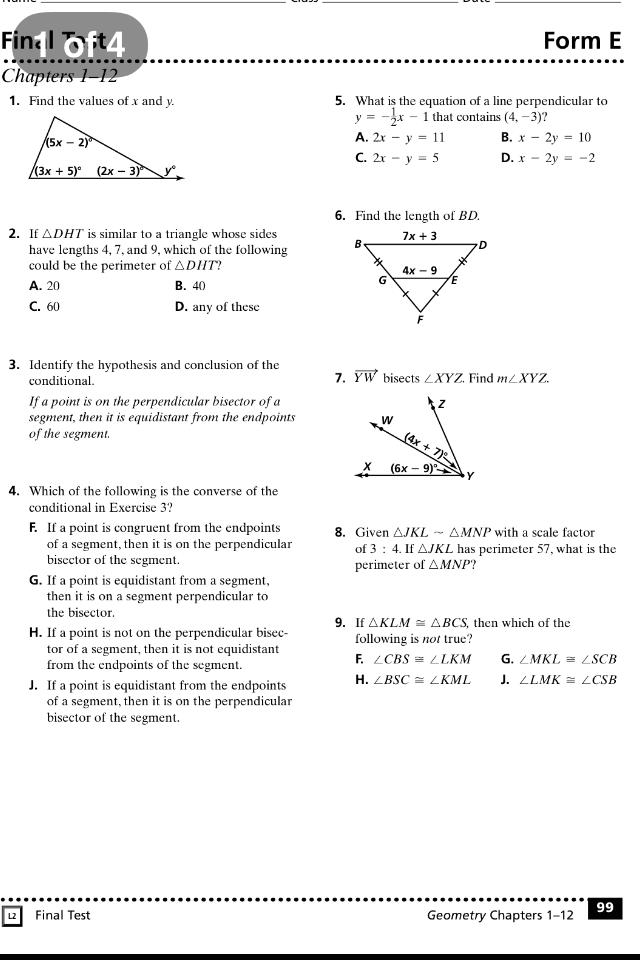
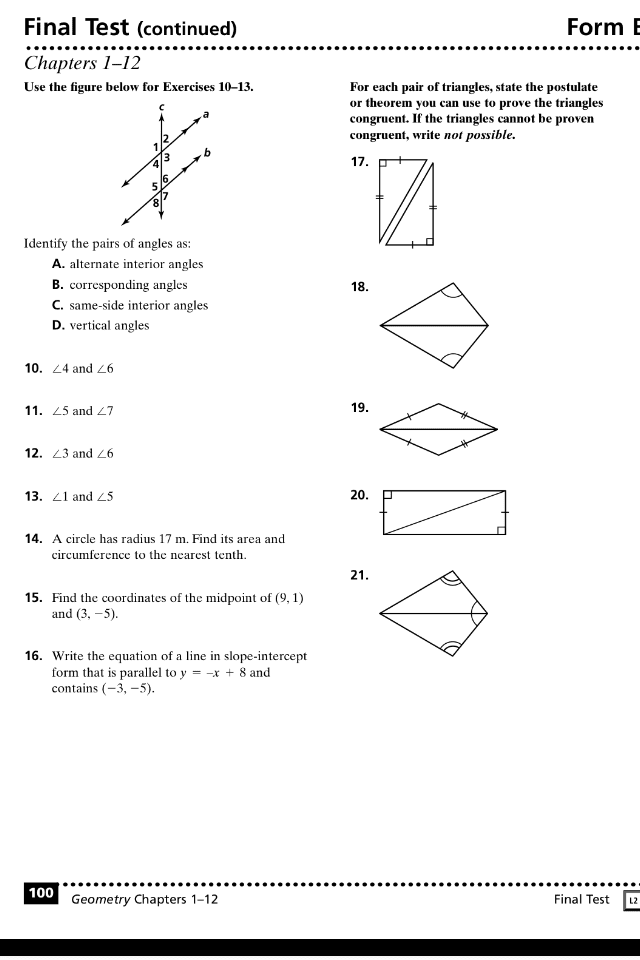
MATH 3050 Study Guide - Quiz Guide: Great Circle, Holonomy, Prentice Hall

197 views10 pages

27 May 2015

School

York University

Department

Mathematics and Statistics

Course

Professor

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

In this assignment we will show that how the area of a triangle on a sphere is calculated. This is done by at first introducing lune on a sphere and its area with respect to its angle. Later on, a formula is calculated and proved which it depends on the interior angles of the triangle and . Gauss-bonnet formula and holonomy of a simple convex polygon on a hemisphere. Formulas will be proved and again this formula will be with respect to sum of the interior or exterior angles of the polygon. two great circles. Meaning it is any four region of the sphere that is created by the intersection of two great circles. The angles of a lune are all congruent by symmetry and vat and also the angle of the lune is the angle between the two great circles. As it is shown in the diagram below:

Related textbook solutions

Calculus

ISBN: 9781319050733

Single Variable Calculus: Early Transcendentals

4th Edition, 2018

ISBN: 9781337687805

CALCULUS:EARLY TRANSCENDENTALS

ISBN: 9781319050740

Related Documents

MATH 3050 Study Guide - Quiz Guide: Isosceles Triangle, Great Circle, Prq

MATH 3050 Study Guide - Quiz Guide: Linear Algebra, Prentice Hall, Daina Taimina

MATH 3050 Study Guide - Quiz Guide: Screw Axis, Isometry, Great Circle

Related Questions

General Math Terms A product B. digit C. numeral D. compass E. equation F. formula G. negative H. sum I. mean J. statistics K. positive L. percent M. straight-edge N. squareroot O. quotient P. prime numbers Q. difference R. addend S. minuend T. divisor Greater than zero: plus. A number being added to another number. A mathematical sequence whose verb is equal (=). The result of addition. The number doing the dividing in a division problem. An instrument used to construct straight lines. A mathematical expression of a natural law. The result of multiplication. The number from which another number is being subtracted. Any non-negative numeral less than ten. Less than zero: minus. An instrument used to construct circles and arcs of circles. A number that produces another number (it's square) when multiplied by itself. The result of subtraction. A symbol or name of a number. The average: the sum of the elements divided by the number of elements. The result of division. Parts per hundred: hundredths. Natural numbers greater than one that have no other factors except one and themselves. Set of numerical data. Geometry A. chord B. diameter C. radius D. perimeter E. cylinder F. surface area G. right angle H. square I. Hypotenuse J. obtuse angle K. vertex L point M. ray N. bisect O arc P. hexagon Q. pentagon R. polygon S. perpendicular T. rectangle U. rhombus V. triangle W. circumference X cube Y pyramid Z. sphere A six-sided polygon. The common end point of the sides of an angle. An angle measuring more than 90 degree. A long, round object with flat, circular ends. An angle of 90 degree. The side of a right triangle opposite the right angle. The total area of all the surfaces of an object. To multiply a number by itself. A location, the place where two lines cross or intersect. A closed geometric figure made up of three or more line segments. The perimeter of a circle: the distance around a circle. A shape having the same dimensions of length, height, and width. A half-line with a designated end point which extends in only one direction without stopping. A figure having a polygon base and triangular sides which meet in a point at the top. Divide an angle into two equal angles. A part of a circle

j

PLEASE NEED HELP WITH THIS TEST!!!

Use the figure below for Exercises 32-34. Find m 2 if mST = 132. Find m 4 if mRQT = 136. Find mQTS if m 1 = 27 and m 2 = 60. Classify the triangle as right, acute, or obtuse if the measures of its sides are 31, 45, and 56. Find the center and radius of the circle with equation (x + 6)2 + (x - 5)2 = 64. Find the lengths of MW- and MX-. Round your answers to the nearest tenth. Find the area of the trapezoid. Find the value of x if BD = 8 and BC = 17. Find the area of an equilateral triangle with perimeter of 60 in. Round your answer to the nearest hundredth. Find the values of x and y. Leave your answers in simplest radical form. The lengths of the sides of a right triangle are 18 ft. 24 ft. and 30 ft. What is the area of the triangle? 216 ft2 270 ft2 432 ft2 cannot be determined Find the volume of the cylinder in terms of pi. Find the value of x. Determine which of the following will tessellate. Decagon pentagon octagon triangle Determine the angle of rotation of Figure 1 to Figure 2. Figure 1 Figure 2 Given CKMS ~ DLNT. If the area of CKMS is 32 cm2, what is the area of DLNT? Find the height of a regular square prism with base edge of 6 ft and volume of 504 ft 3. What is the distance between (-12.6) and (8, -9)? Find the value of x. Assume that segments that appear to be tangent are tangent. 40 50 60 100 Find the values of x and y. If Delta DHT is similar to a triangle whose sides have lengths 4, 7, and 9. which of the following could be the perimeter of Delta DHT? 20 40 60 any of these Identify the hypothesis and conclusion of the conditional. If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment. Which of the following is the converse of the conditional in Exercise 3? If a point is congruent from the endpoints of a segment, then it is on the perpendicular bisector of the segment. If a point is equidistant from a segment, then it is on a segment perpendicular to the bisector. If a point is not on the perpendicular bisector of a segment, then it is not equidistant from the endpoints of the segment. If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment. What is the equation of a line perpendicular to that contains (4, -3)? 2x - y = 11 x - 2y = 10 2x - y = 5 x - 2y = -2 Find the length of BD. YW rightarrow bisects . Find m . Given Delta JKL ~ Delta MNP with a scale factor of 3 : 4. If Delta JKL has perimeter 57, what is the perimeter of Delta MNP? If Delta KLM Delta BCS, then which of the following is not true? Use the figure below for Exercises 10-13. Identify the pairs of angles as: alternate interior angles corresponding angles same-side interior angles vertical angles A circle has radius 17 m. Find its area and circumference to the nearest tenth. Find the coordinates of the midpoint of (9, 1) and (3, -5). Write the equation of a line in slope-intercept form that is parallel to y = - x + 8 and contains (-3 ,-5). For each pair of triangles, state the postulate or theorem you can use to prove the triangles congruent. If the triangles cannot he proven congruent, write not possible.

Show transcribed image text Use the figure below for Exercises 32-34. Find m 2 if mST = 132. Find m 4 if mRQT = 136. Find mQTS if m 1 = 27 and m 2 = 60. Classify the triangle as right, acute, or obtuse if the measures of its sides are 31, 45, and 56. Find the center and radius of the circle with equation (x + 6)2 + (x - 5)2 = 64. Find the lengths of MW- and MX-. Round your answers to the nearest tenth. Find the area of the trapezoid. Find the value of x if BD = 8 and BC = 17. Find the area of an equilateral triangle with perimeter of 60 in. Round your answer to the nearest hundredth. Find the values of x and y. Leave your answers in simplest radical form. The lengths of the sides of a right triangle are 18 ft. 24 ft. and 30 ft. What is the area of the triangle? 216 ft2 270 ft2 432 ft2 cannot be determined Find the volume of the cylinder in terms of pi. Find the value of x. Determine which of the following will tessellate. Decagon pentagon octagon triangle Determine the angle of rotation of Figure 1 to Figure 2. Figure 1 Figure 2 Given CKMS ~ DLNT. If the area of CKMS is 32 cm2, what is the area of DLNT? Find the height of a regular square prism with base edge of 6 ft and volume of 504 ft 3. What is the distance between (-12.6) and (8, -9)? Find the value of x. Assume that segments that appear to be tangent are tangent. 40 50 60 100 Find the values of x and y. If Delta DHT is similar to a triangle whose sides have lengths 4, 7, and 9. which of the following could be the perimeter of Delta DHT? 20 40 60 any of these Identify the hypothesis and conclusion of the conditional. If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment. Which of the following is the converse of the conditional in Exercise 3? If a point is congruent from the endpoints of a segment, then it is on the perpendicular bisector of the segment. If a point is equidistant from a segment, then it is on a segment perpendicular to the bisector. If a point is not on the perpendicular bisector of a segment, then it is not equidistant from the endpoints of the segment. If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment. What is the equation of a line perpendicular to that contains (4, -3)? 2x - y = 11 x - 2y = 10 2x - y = 5 x - 2y = -2 Find the length of BD. YW rightarrow bisects . Find m . Given Delta JKL ~ Delta MNP with a scale factor of 3 : 4. If Delta JKL has perimeter 57, what is the perimeter of Delta MNP? If Delta KLM Delta BCS, then which of the following is not true? Use the figure below for Exercises 10-13. Identify the pairs of angles as: alternate interior angles corresponding angles same-side interior angles vertical angles A circle has radius 17 m. Find its area and circumference to the nearest tenth. Find the coordinates of the midpoint of (9, 1) and (3, -5). Write the equation of a line in slope-intercept form that is parallel to y = - x + 8 and contains (-3 ,-5). For each pair of triangles, state the postulate or theorem you can use to prove the triangles congruent. If the triangles cannot he proven congruent, write not possible.

mauvemuskrat666

number 1