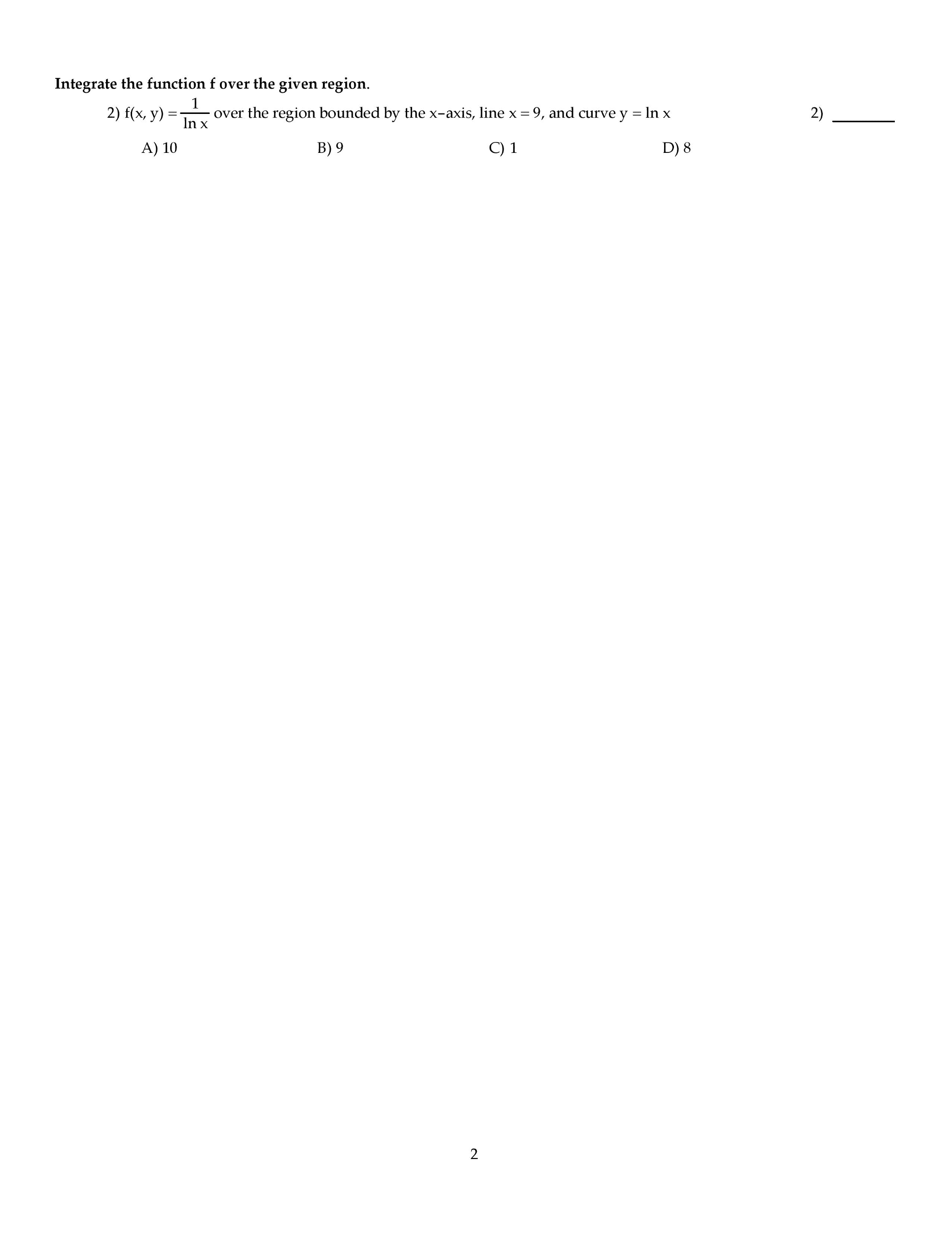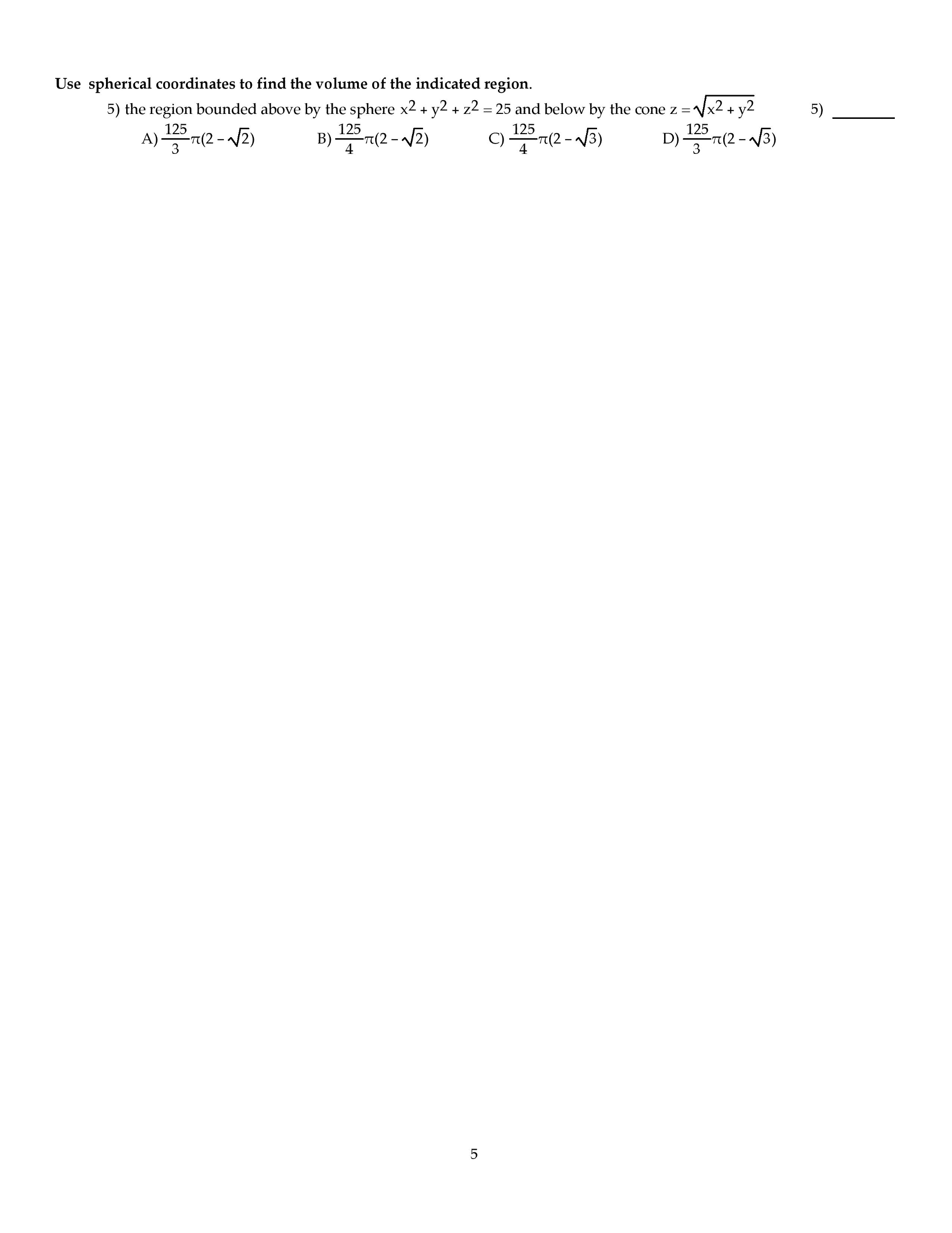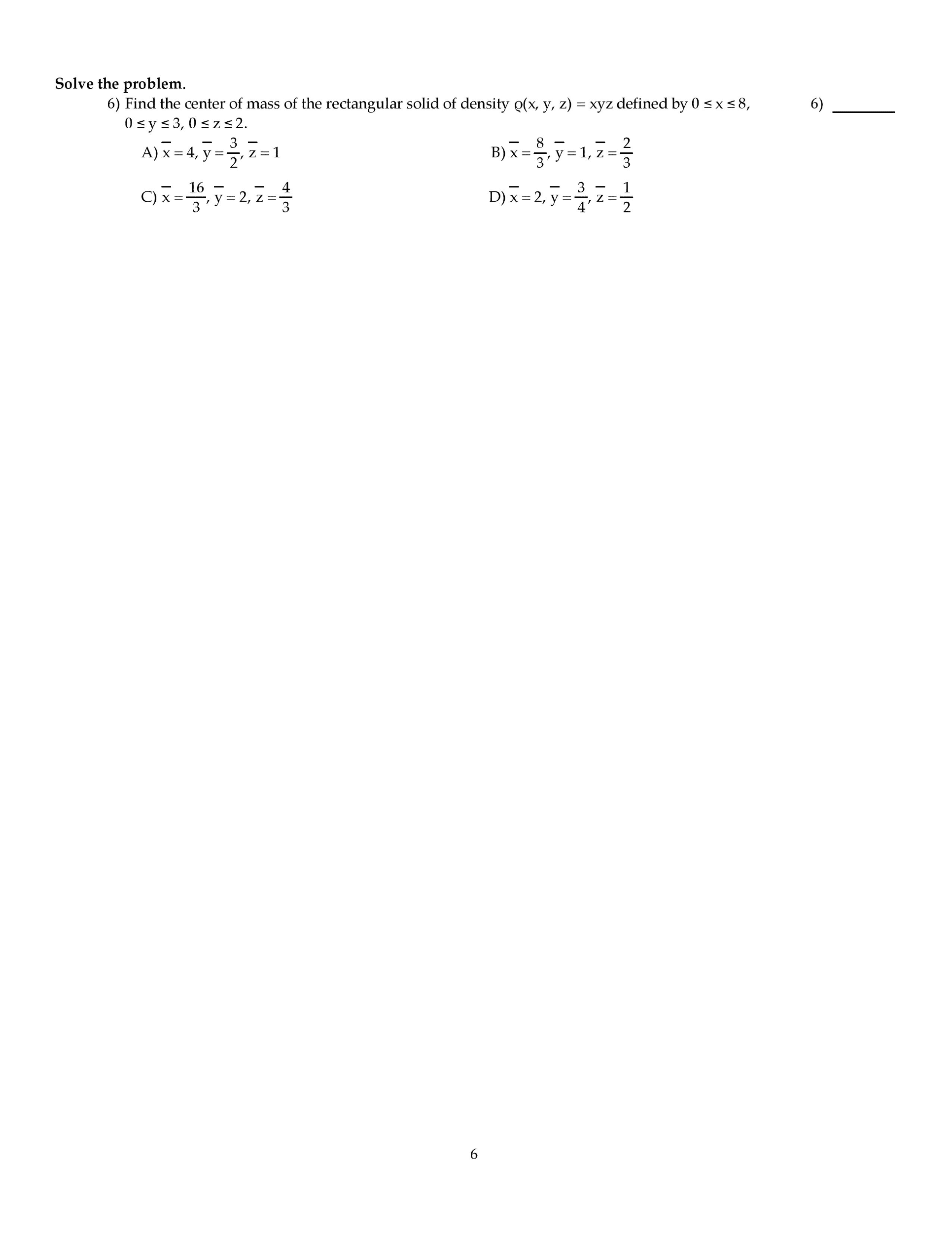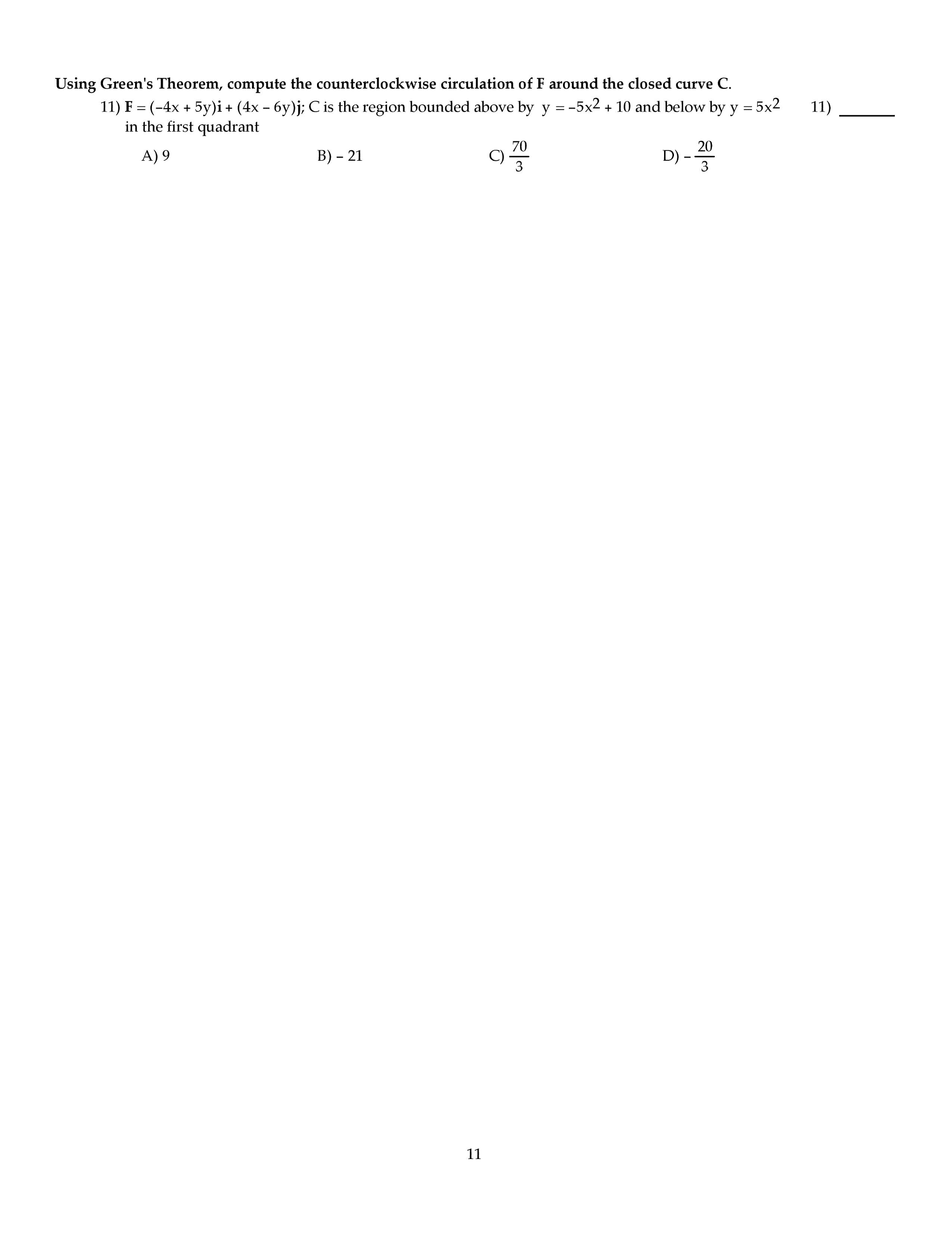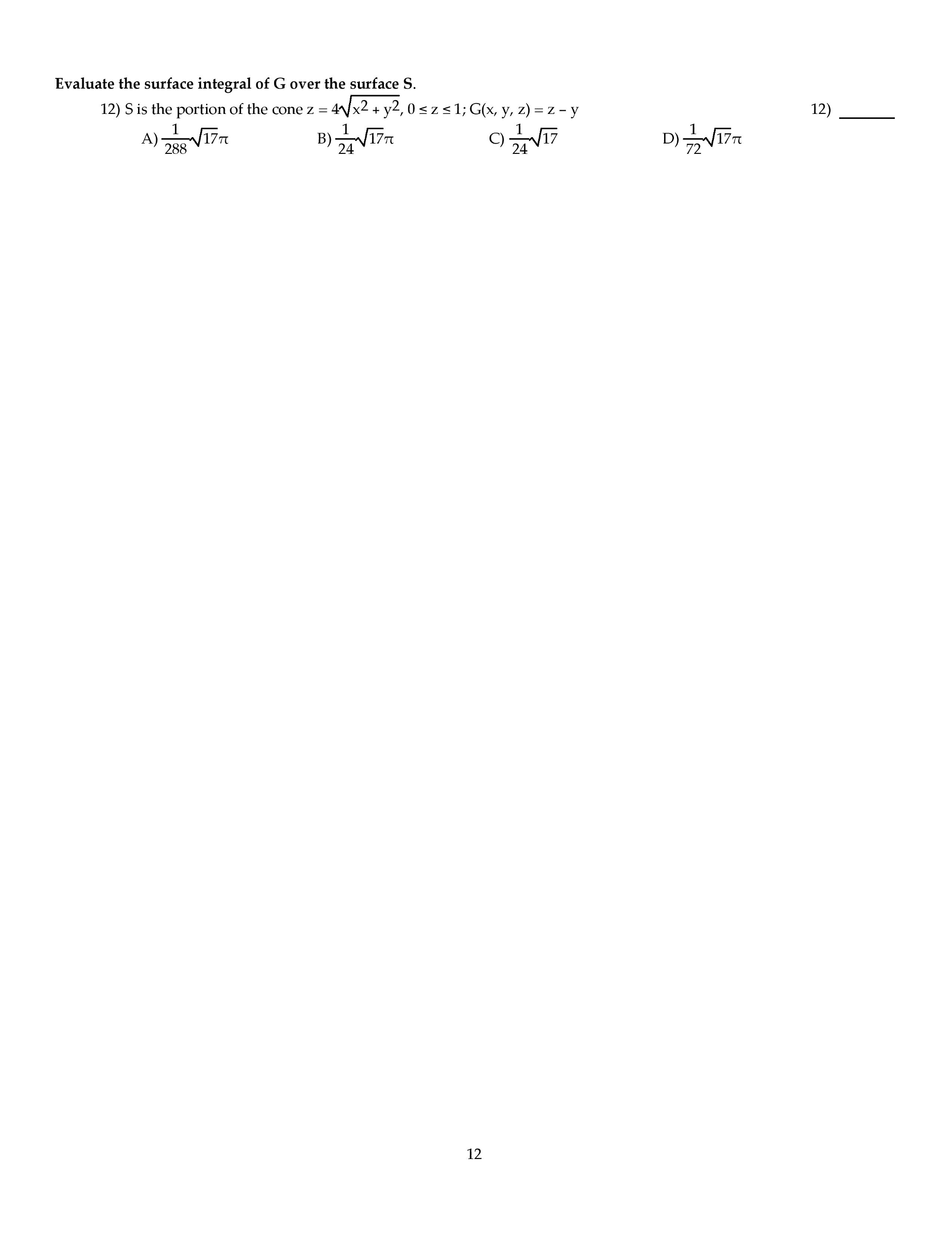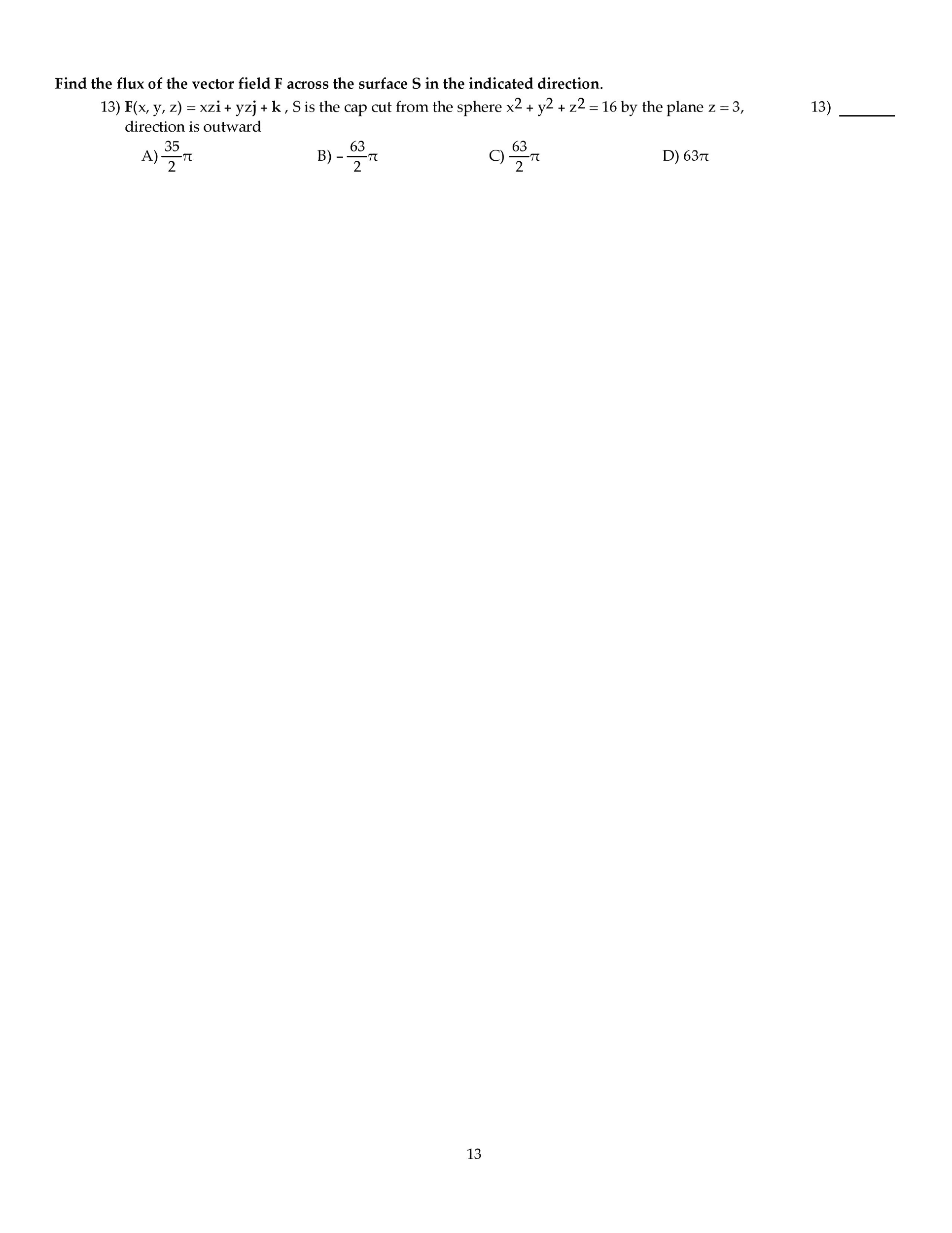MAT223H1 Study Guide - Midterm Guide: Row Echelon Form, Euclidean Vector, Scalar Multiplication
Document Summary
November 15, 2013: crooks, m. mota, c. park, s. uppal, f. vera-pacheco, y. zong. Has reduced echelon form: suppose you are given that the matrix a = [9] (b) find a basis for each of the following three subspaces: (i) row(a), (ii) col(a), and (iii) null(a). Solution: (a) rank(a) = number of leading variables in r = 3. (b) (i) the rows of r with leading variables in them form a basis for row(a): {(cid:2)1 2 0 0(cid:3) ,(cid:2)0 0 1 0(cid:3) ,(cid:2)0 0 0 1(cid:3)}. (ii) the columns of a corresponding to the columns of r with leading variables in them form a basis for a basis for col(a): 0 (t r). (iii) there"s one free parameter (corresponding to x2) and x is in null(a) if and only if x = So a basis for null(a) is: (note that this is inline with the rank-nullity theorem: 4 = rank(a) + nullity(a) = 3 + 1. )