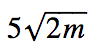MATA33H3 Study Guide - Final Guide: Matrix Addition, Coefficient Matrix, Saddle Point
MATA 33 STUDY GUIDE
FINAL EXAM 2018

Chapter 7 – Linear Programming, Matrix Algebra, Calc. of Several Variables
7.1 – Linear Programming
IDEA: we consider a linear function of 2 variables,
F ( x , y ) = ax + by a , b E R (constant)
We study how to maximize (max/min) F , where x and y are subject to a set of linear inequalities.
NOTATION:

How to draw the graph of linear function:
Intercepts: Y – ( 0 , b ) put x = 0
X – ( - b/m , 0 ) put y = 0 , fine if m does not equal 0.
m = 0 y = b is a horizontal line

3
MATA33H3 Full Course Notes
Verified Note
3 documents
Document Summary
Chapter 7 linear programming, matrix algebra, calc. of several variables. Idea: we consider a linear function of 2 variables, F ( x , y ) = ax + by a , b e r (constant) We study how to maximize (max/min) f , where x and y are subject to a set of linear inequalities. How to draw the graph of linear function: Y ( 0 , b ) put x = 0. X ( - b/m , 0 ) put y = 0 , fine if m does not equal 0. m = 0 y = b is a horizontal line. This is simply several inequalities at the same time. Given a linear inequality, the solution to it (or the feasible set for it) is the set of all points (x,y) in the plane r^2 that satisfies the given inequality. The function to be max/min is called the objective function.