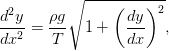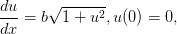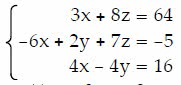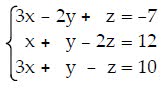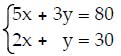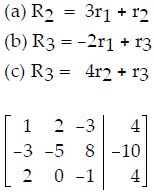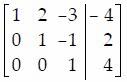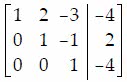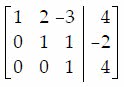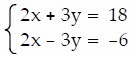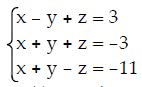MATH 401 Midterm: MATH 401 2008 Winter Test 2

43 views2 pages

turquoisegnu128

9 Jan 2019

School

Department

Course

Professor

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

Answer all questions; time 2. 5 hours: [17] consider the problem. L[u] = ut uxx = f (x, t), 0 < x < ; t > 0, u(x, 0) = g(x); ux(0, t) = 1; u 0, x . Derive the solution for the problem using the green"s function from rst principles. F ( , , x, t) = (4 (t ))1/2 exp( ( x)2. 4(t ) where h(t ) is the unit step function: [16] consider the functional. {(u00)2 ug(x)}dx, where g(x) is a given function. Determine, from rst principles, the di erential equation and natural bound- ary conditions that u(x) must satisfy to minimize the functional. 1: [16] the region d is the triangle bounded by the lines, y = x/ 3 and x = 3, and uxx + uyy + 2 = 0 in d, (1) u = 0 on boundary of d, Describe how you would nd approximate solutions to (1) using galerkin,

Related Questions

Using a technique of integration and the separation-of-variables technique, you'll discover a function whose antiderivative models the shape of an ideal cable suspended from its endpoints. The function depends on a parameter b, which is determined by the properties of the cable, such as the density of the material out of which it is made.

Using principles from physics, it can be shown that when a perfectly flexible, uniformly dense, and inextensible cable is suspended from its endpoints, then it will assume a shape of a curve y = f(x) satisfying the following second-order differential equation:

where Ï is the density of the material of the cable, g is the acceleration due to gravity, and T is the magnitude of the tension in the cable at its lowest point.

We assume our cable is as in the diagram above and y = f(x) is its shape function; thus, not only does y satisfy the "hanging cable differential equation" above, we also have y '(0) = 0. Hence, making the substitution u =dy/dx in our the hanging cable equation, we obtain the first order, initial-value problem satisfied by u:

where b = Ïg/T Solve the preceding initial-value problem, entering your (explicit) solution in the form u = g(x) where g is a function of x in which the constant b is present.

I need help with these as soon as possible Please. Thank You!!

Q15. In 1990, the population of a country was estimated at 4 million. For any subsequent year the population, P(t) (in millions), can be modeled by the equation P(t) = 240/(5 + 54.99e^-0.0208t), where t is the number of years since 1990. Estimate the year when the population will be 21 million.
a. approximately the year 2093
b. approximately the year 2041
c. approximately the year 2088
d. approximately the year 2016

Q18. A size 6 dress in Country C is size 52 in Country D. A function that converts dress sizes in Country C to those in Country D is f(x) = 2(x + 20). Find a formula for the inverse of the function described.
a. f ^-1(x) = (x - 20)/2
b. f ^-1(x) = x - 20
c. f ^-1(x) = (x/2) - 20
d. f ^-1(x) = (x/2) + 20

Q19. If f(x) = 4^x and g(x) = 12, find the point of intersection of the graphs of f and g by solving f(x) = g(x). Give an exact answer.
a. (log ₄ 12, 12)
b. (log ₄ 12, 4)
c. (log ₄ 12, 0)
d. (12, 12)

Q20. Find functions f and g so that f â g = H(x) = (5 - 2x³)².
a. f(x) = 5 - 2x³ ; g(x) = x²
b. f(x) = (5 - 2x)³ ; g(x) = x²
c. f(x) = x² ; g(x) = 5 - 2x³
d. f(x) = x³ ; g(x) = (5 - 2x)²

Q29. Solve the system of equations using Cramer's Rule if it is applicable.

a. x = 9, y = 2, z = 5; (9, 2, 5)
b. x = 8, y = 4, z = 5; (8, 4, 5)
c. x = 4, y = 5, z = 4; (4, 5, 4)
d. x = 8, y = -4, z = -5; (8, -4, -5)

Q30. Solve the system of equations using matrices (row operations). If the system has no solution, say that it is inconsistent.

a. x = 2, y = 3, z = -7; (2, 3, -7)
b. x = 1, y = 3, z = -4; (1, 3, -4)
c. x = 5, y = 13/2, z = -3; (5, 13/2, -3)
d. x = 1, y = -3, z = -16; (1, -3, -16)

Q33. Write the partial fraction decomposition of the rational expression (4x³ + 4x²)/(x² + 5)².
a. (4x - 4)/(x² + 5) + (-20x + 20)/(x² + 5)²
b. (4x + 4)/(x² + 5) + (-20x - 20)/(x² + 5)²
c. (4x + 4)/(x² + 5) + (20x - 20)/(x² + 5)²
d. (4x + 4)/(x² + 5) + (20x + 20)/(x² + 5)²

Q34. Solve the linear programming problem. Minimize z = 11x + 6y + 7 subject to: x = 0, y = 0, x + y = 1.
a. minimum: 7
b. minimum: 18
c. minimum: 24
d. minimum: 13

Q35. Solve the system of equations by elimination.

a. x = 10, y = 0; (10, 0)
b. x = 10, y = 10; (10, 10)
c. x = 0, y = 10; (0, 10)
d. x = 0, y = 0; (0, 0)

Q36. Perform the row operations on the given augmented matrix.

a.
b.
c.
d.

Q37. Solve the system of equations using Cramer's Rule if it is applicable.

a. x = -4, y = 3; (-4, 3)
b. x = -3, y = -4; (-3, -4)
c. x = 4, y = 3; (4, 3)
d. x = 3, y = 4; (3, 4)

Q38. Write the partial fraction decomposition of the rational expression x/(x² - 9x + 20).
a. -4/(x - 4) + 5/(x - 5)
b. -5/(x - 4) + 4/(x - 5)
c. 4/(x - 4) + -5/(x - 5)
d. -4/(x - 4) + -5/(x - 5)

Q39. Solve the system of equations.

a. x = -4, y = 4, z = -3; (-4, 4, -3)
b. x = -3, y = 4, z = -4; (-3, 4, -4)
c. x = -4, y = -3, z = 4; (-4, -3, 4)
d. inconsistent

Q40. Find the value of the determinant.

a. 224
b. 24
c. -72
d. 72