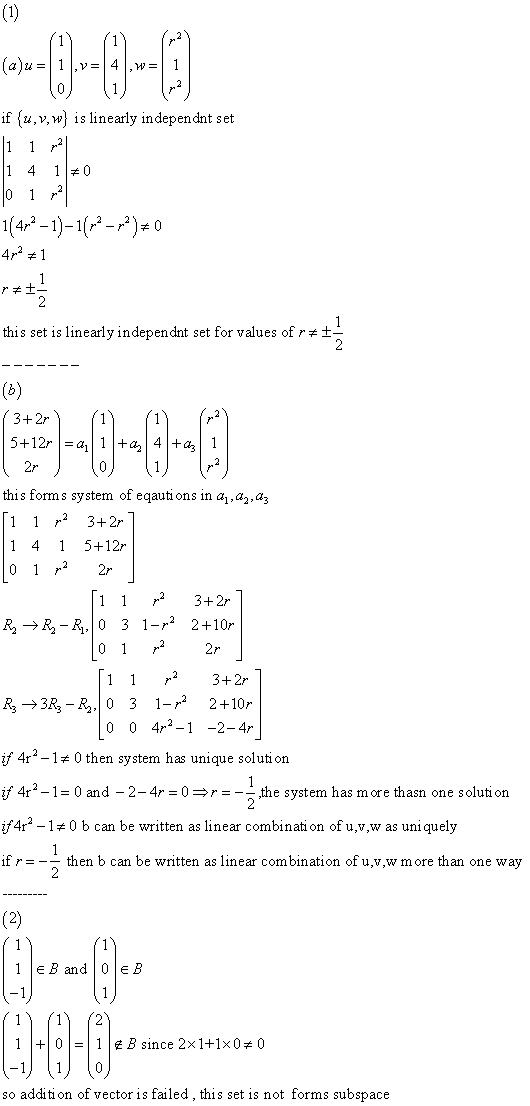MATH 381 Midterm: MATH 381 McGill Examf96
Document Summary
Mathematics 189-354a: (a) let (x, d1) and (y, d2) be metric spaces. Suppose (x, d) is a complete metric space. Let g1, g2, . be a sequence of open subsets of x. Suppose, in addition, gn is dense in x, for each n. prove that is also dense in x. Gn: let (fn) be a uniformly bounded sequence of functions which are riemann integrable fn(t)dt, a x b, prove that there exists a subsequence on [a, b]. [hint: let {x1, x2, . be a subset of x; if fn(x) = d(x, xn) for all x x, then. {1, f1, f2, . generates an algebra in c(x, r). ] Prove that f 1 is di erentiable on v . (b) let u be an open set in rn, let u0 u and let f : u rn be continuous on u. Df(x) = l, prove that f is and continuously di erentiable on u\{u0}.