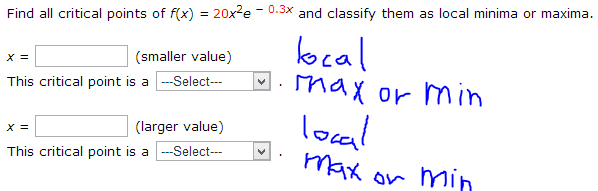
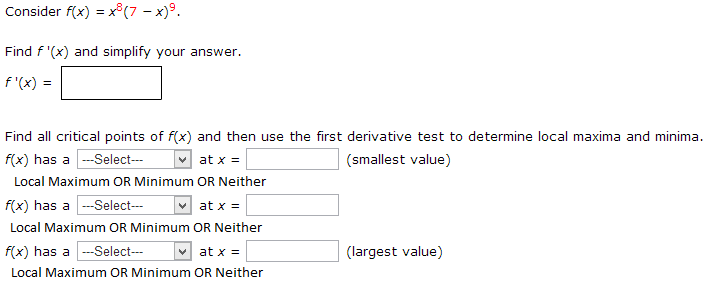
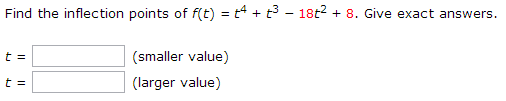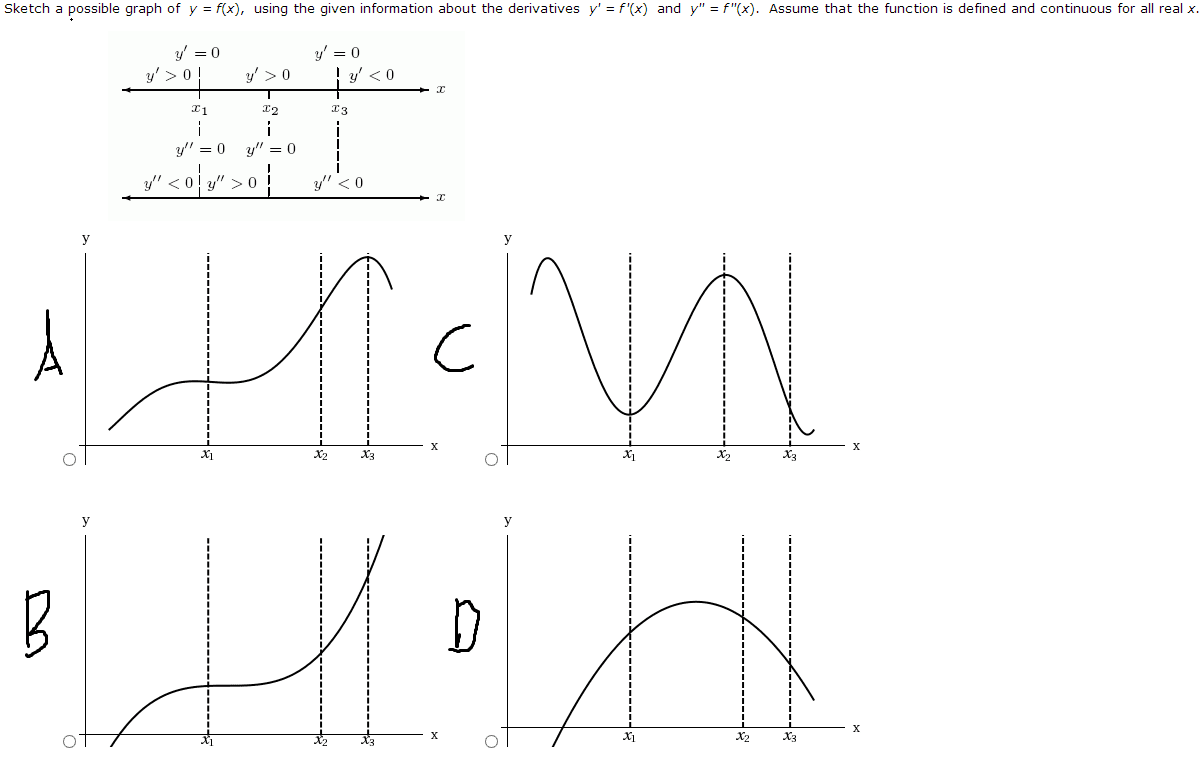1
answer
0
watching
86
views
13 Nov 2019
Let f(x) = 1 x and g(x) = 1 x if x > 0 4 + 1 x if x < 0 Show that fâ'(x) = g'(x) for all x in their domains. Can we conclude from the corollary below that f â g is constant? If fâ'(x) = g'(x) for all x in an interval (a, b), then f â g is constant on (a, b); that is, f(x) = g(x) + c where c is a constant.
Let f(x) = 1 x and g(x) = 1 x if x > 0 4 + 1 x if x < 0 Show that fâ'(x) = g'(x) for all x in their domains. Can we conclude from the corollary below that f â g is constant? If fâ'(x) = g'(x) for all x in an interval (a, b), then f â g is constant on (a, b); that is, f(x) = g(x) + c where c is a constant.
1
answer
0
watching
86
views
For unlimited access to Homework Help, a Homework+ subscription is required.
Tod ThielLv2
16 May 2019