L24 Math 132 Lecture 25: Series
Document Summary
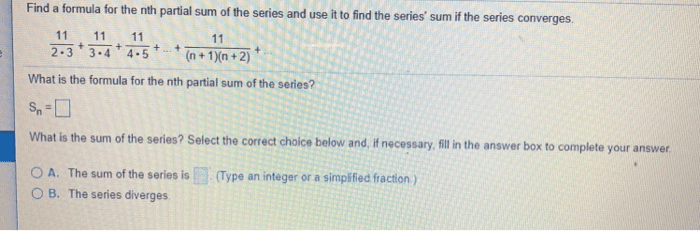
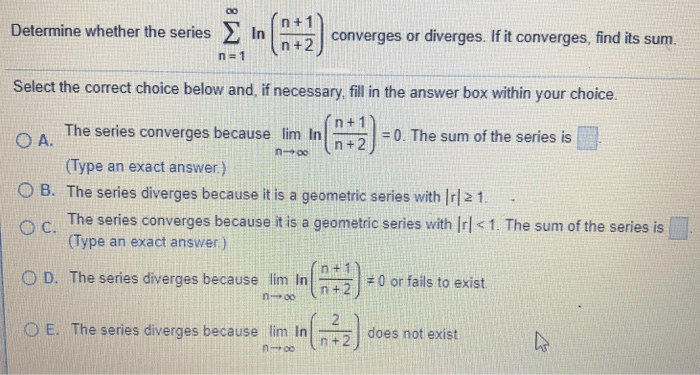
An infinite sum of numbers (sum of the terms of a sequence) Sn = a1 + a2 + a3 + + an. If lim(cid:3041) (cid:2998)(cid:1845)(cid:3041)=(cid:1838) then we say the series converges and is equal to the limit. If the limit does not exist, then the series diverges. A geometric series is of the form: (cid:2998)(cid:3041)(cid:2880)(cid:2868) (cid:1853)(cid:1870)(cid:3041) Where a and r are constants, a is not equal to 0: formula for sn: = a + a + a + + a*1n. = a(n+1) r = 1, sn = a + a*1 + a*12 + + a*1n r = -1, sn = a + -1a + (-1)2a + (-1)na. = a a + a + (-1)na. = a for odd n, 0 for even n. All other r, sn = a + ar + ar2 + + arn rsn= ar + ar2 + + arn + arn+1.
