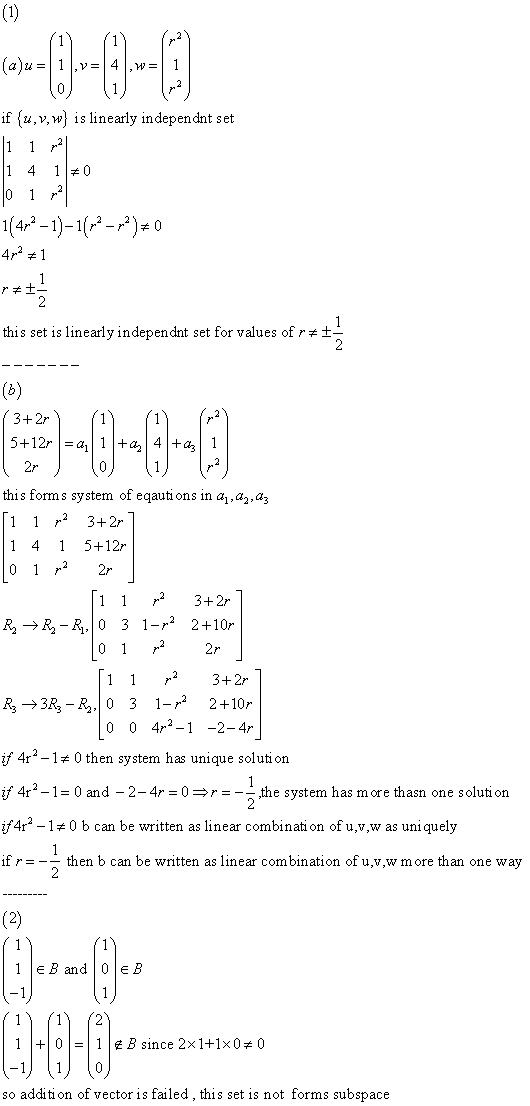HomeClass Notes1,200,000US530,000

MATH 2574H Lecture : Discussion 3252014.pdf

37 views6 pages

mauvedinosaur421

15 Jul 2014

School

Department

Course

Professor

For unlimited access to Class Notes, a Class+ subscription is required.

Document Summary

Span: the span of vectors is all linear combinations of them. Span{v1, v2, v3} c1v1 + c2v2 + c3v3 span{v1, v2, v3} A vector space (any vector space) can be written as a span of some vectors. Find the vectors spanning a solution space (kernel). Basis: the set of vectors that span the vector space. So in span{v1, v2, v3}, those 3 vectors are the basis. If leave the 3rd one out, won"t span the space. Can contain redundant vectors, but can"t contain a vector that"s not in the space. Basis of r2 (where r is being used for all real #s) Find a basis for kernel x3 = s x2 + 5s = 0 --> x2 = -5s x1 - 11s = 0 --> x1 = 11s. How to tell if vectors are linearly independent. They are linearly independent if only has the zero solution; has.

Related textbook solutions

Calculus

ISBN: 9781319050733

Single Variable Calculus: Early Transcendentals

4th Edition, 2018

ISBN: 9781337687805

CALCULUS:EARLY TRANSCENDENTALS

ISBN: 9781319050740

Related Documents

MATH136 Lecture Notes - Spanx, Linear Combination, Flowchart

ochresquirrel161

MATH136 Chapter 1-6: Math 136.docx

raspberrybeaver721

MATH136 Lecture Notes - Coordinate Vector, Row Echelon Form, Elementary Matrix

chocolateduck372

Related Questions

I have the answer for the following question. But some of theanswers are not correct.

Please do the following question by yourself and check which arethe wrong answers,please post your answers and compare to it.

Let r in and u =(1 1 0), v = (1 4 1), w = (r2 1 r2), b = (3+2r 5+12r 2r). For which values r in is the set {u. v, w} linearly independent? For which values r in is the vector b a linear combination of u. v and w? For which of these values of r can b be written as a linear combination of u. v and w in more than one way? The set 3 of all column vectors of length three, with real entries, is a vector space. Is the subset B = {(x y z) in 3 | xy + yz = 0} a subspace of 3? Justify your answer. Show that the set of all twice differentiable functions f : satisfying the differential equation sin(x) f"(x) + x2f(x) = 0 is a vector space with respect to the usual operations of addition of functions and multiplication by scalars. Here, f" denotes the second derivative of f. Let S be the following subset of the vector space 3 of all real polynomials p of degree at most 3: S = {p in 3 | p(l) = 0, p'(l) = 0}, where p' is the derivative of p. Determine whether S is a subspace of 3. Determine whether the polynomial q(x) = x - 2x2 + x3 is an element of S. u = (1 1 0), v = (1 4 1), w = (r2 1 r2) if {u, v, w} is linearly independent set 1(4r2 - 1)-1(r2 - r2) ne 0 4r2 ne 1 r ne plusmn1/2 this set is linearly independent set for values of e ne plusmn1/2 - - - - - - - (3+2r 5+12r 2r) = a1 (1 1 0) + a2 (1 4 1) + a3 (r2 1 r2) this forms system of equations in a1, a2, a3 if 4r2 - 1 ne 0 then system has unique solution if 4r2 - 1 = 0 and -2 - 4r = 0 rArr r = -1/2, the system has more than one solution if 4r2 - 1 ne 0 b can be written as linear combination of u,v,w as uniquely if r = -1/2 then b can be written as linear combination of u,v,w more than one way - - - - - - - - - (1 1 -1) in B and (1 0 1) in B (1 1 -1) + (1 0 1) = (2 1 0) not in B since 2times1+1times0 ne 0 so addition of vector is failed, this set is not forms subspace consider the following differential equation (sinx)f"(x) + x2f (x) = 0 each solution is continuous function the set of all solutions is subset of space of set of all continuous functions n from R to R let f,g are two solutions (sinx)f"(x) + x2f (x) = 0 (sinx)g"(x)+x2g(x) = 0 ccheck whether af+bg is solution or not (sinx)f"(x) + x2f(x) = 0 rArr (sinx) af"(x) + x2?f (x) = 0 (sinx)g"(x) + x2g (x) = 0 rArr (sinx)bg" (x) + x2bg (x) = 0 (sinx)(af"(x)+bg"(x)) +x2 (af (x) + bg(x)) = 0 af+bg is also solution to differential equation the set of all solutions to differential equation forms subspace - - - - - - - - - - consider the following subset of P3 {p in P3/.p(l)=0, p'(l) = 0} let p, q in S rArr p(l)= 0, p'(l) = 0 and q(l) = 0, q'(l) = 0 (ap + bq) (l) = ap (l) +b q(l) = a (0) + b (0) = 0 (ap + bq)'(1) = ap'(l) +bq'(1) = a (0) + b(0) = 0 p, q in S rArr ap +bq in S then S is subspace q(x) = x - 2x2 + x3 q(1) = 1 - 2 + 1 = 0 q'(x)=1 - 4x + 3x2 q'(l) = 1 - 4 + 3 = 0 q is element of S