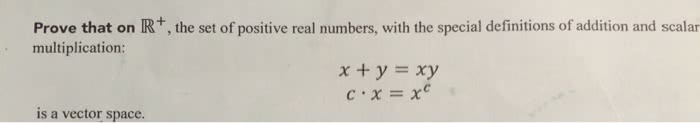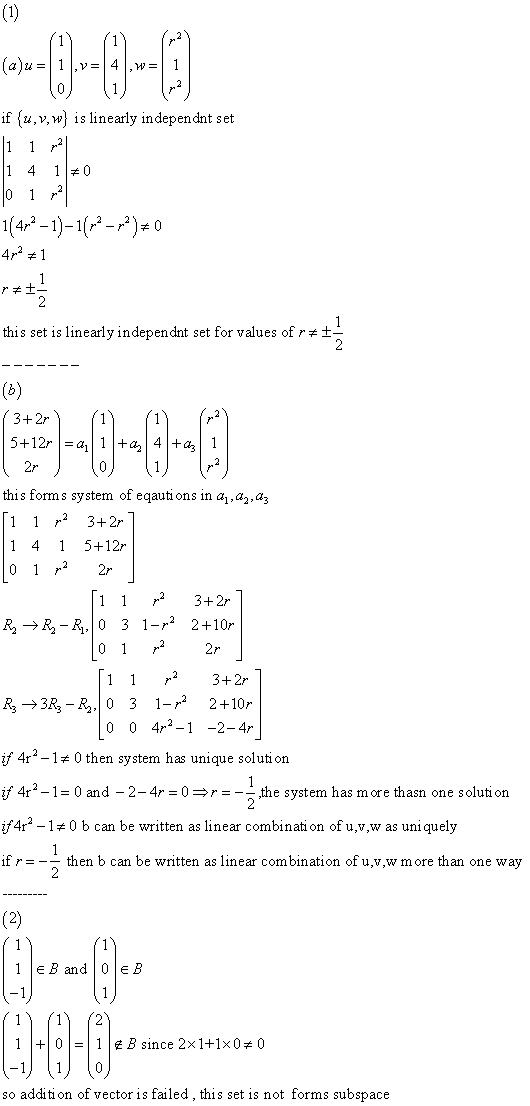HomeClass Notes1,200,000US530,000

MATH 21 Lecture Notes - Lecture 3: Zero Element, Distributive Property, Additive Inverse

19 views4 pages

20 Jul 2018

School

Department

Course

Professor

For unlimited access to Class Notes, a Class+ subscription is required.

Document Summary

Components: entries that appear in a vector. By n-space, mean the collection of all n-vectors. If m n then irm and irn have no elements in common. Two n-vectors are equal if and only if all components are identical. To add two n-vectors, add the corresponding components of each vector. Scalar multiple vector is obtained by multiplying each component by the scalar multiple. Negative or opposite is the vector multiplied by scalar multiple (-1) Zero vector is vector whose every entry is zero i where 1 i n has all zeros except the ith component which is a 1. Theorem: let u, v, w irn and a, b ir. The following hold: (1) (u + v) + w = u + (v + w) addition is associative (2) u + v = v + u (3) u + 0n = u (4) u + (-u) = 0n.

Related textbook solutions

Calculus

ISBN: 9781319050733

Single Variable Calculus: Early Transcendentals

4th Edition, 2018

ISBN: 9781337687805

CALCULUS:EARLY TRANSCENDENTALS

ISBN: 9781319050740

Related Documents

MATH 21 Lecture Notes - Lecture 7: Row Echelon Form, Dot Product, Coordinate Vector

MATH 21 Lecture Notes - Lecture 5: Coefficient Matrix, Linear Combination, Subsequence

MATH 21 Lecture Notes - Lecture 6: Gaussian Elimination, Scalar Multiplication

Related Questions

By using the definition of a vector space

How do I prove this?

Show transcribed image text

scarletmallard305

I have the answer for the following question. But some of theanswers are not correct.

Please do the following question by yourself and check which arethe wrong answers,please post your answers and compare to it.

Let r in and u =(1 1 0), v = (1 4 1), w = (r2 1 r2), b = (3+2r 5+12r 2r). For which values r in is the set {u. v, w} linearly independent? For which values r in is the vector b a linear combination of u. v and w? For which of these values of r can b be written as a linear combination of u. v and w in more than one way? The set 3 of all column vectors of length three, with real entries, is a vector space. Is the subset B = {(x y z) in 3 | xy + yz = 0} a subspace of 3? Justify your answer. Show that the set of all twice differentiable functions f : satisfying the differential equation sin(x) f"(x) + x2f(x) = 0 is a vector space with respect to the usual operations of addition of functions and multiplication by scalars. Here, f" denotes the second derivative of f. Let S be the following subset of the vector space 3 of all real polynomials p of degree at most 3: S = {p in 3 | p(l) = 0, p'(l) = 0}, where p' is the derivative of p. Determine whether S is a subspace of 3. Determine whether the polynomial q(x) = x - 2x2 + x3 is an element of S. u = (1 1 0), v = (1 4 1), w = (r2 1 r2) if {u, v, w} is linearly independent set 1(4r2 - 1)-1(r2 - r2) ne 0 4r2 ne 1 r ne plusmn1/2 this set is linearly independent set for values of e ne plusmn1/2 - - - - - - - (3+2r 5+12r 2r) = a1 (1 1 0) + a2 (1 4 1) + a3 (r2 1 r2) this forms system of equations in a1, a2, a3 if 4r2 - 1 ne 0 then system has unique solution if 4r2 - 1 = 0 and -2 - 4r = 0 rArr r = -1/2, the system has more than one solution if 4r2 - 1 ne 0 b can be written as linear combination of u,v,w as uniquely if r = -1/2 then b can be written as linear combination of u,v,w more than one way - - - - - - - - - (1 1 -1) in B and (1 0 1) in B (1 1 -1) + (1 0 1) = (2 1 0) not in B since 2times1+1times0 ne 0 so addition of vector is failed, this set is not forms subspace consider the following differential equation (sinx)f"(x) + x2f (x) = 0 each solution is continuous function the set of all solutions is subset of space of set of all continuous functions n from R to R let f,g are two solutions (sinx)f"(x) + x2f (x) = 0 (sinx)g"(x)+x2g(x) = 0 ccheck whether af+bg is solution or not (sinx)f"(x) + x2f(x) = 0 rArr (sinx) af"(x) + x2?f (x) = 0 (sinx)g"(x) + x2g (x) = 0 rArr (sinx)bg" (x) + x2bg (x) = 0 (sinx)(af"(x)+bg"(x)) +x2 (af (x) + bg(x)) = 0 af+bg is also solution to differential equation the set of all solutions to differential equation forms subspace - - - - - - - - - - consider the following subset of P3 {p in P3/.p(l)=0, p'(l) = 0} let p, q in S rArr p(l)= 0, p'(l) = 0 and q(l) = 0, q'(l) = 0 (ap + bq) (l) = ap (l) +b q(l) = a (0) + b (0) = 0 (ap + bq)'(1) = ap'(l) +bq'(1) = a (0) + b(0) = 0 p, q in S rArr ap +bq in S then S is subspace q(x) = x - 2x2 + x3 q(1) = 1 - 2 + 1 = 0 q'(x)=1 - 4x + 3x2 q'(l) = 1 - 4 + 3 = 0 q is element of S