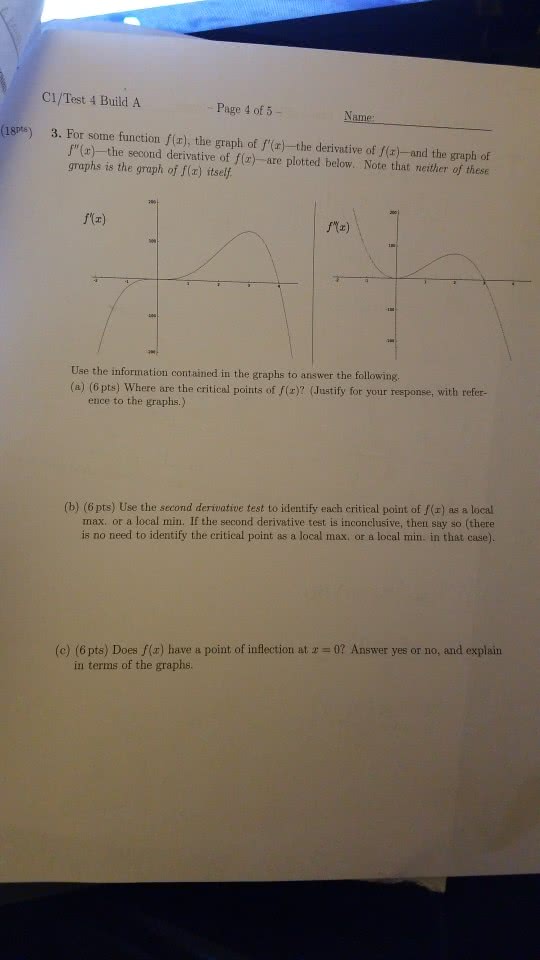
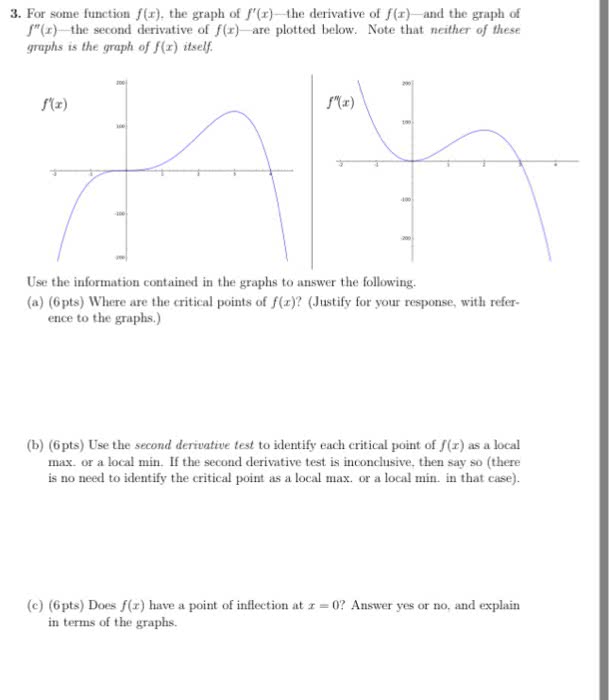
MATH 2A Lecture Notes - Lecture 6: Minimax, Inflection

• School: UC-Irvine
• Department: Mathematics
• Course: MATH 2A
• Professor: Arash Karami

Document Summary

If f is continuous on [a,b], then there must be an absolute max and min. If f has a local max/min at x=c and f"(c) exists, then f"(c) = c. f"=0 or f"=undefined. If f" changes from pos to neg at c, then f has a local max at c. If f" changes from neg to pos at c, then f has a local min at c. If f" has no sign change, then f has no local extreme at c. If f"" > 0 then f has a local min at c. If f"" < 0 then f has a local max at c.