HomeClass Notes1,200,000US530,000

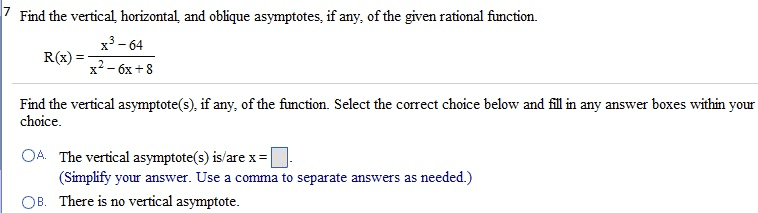
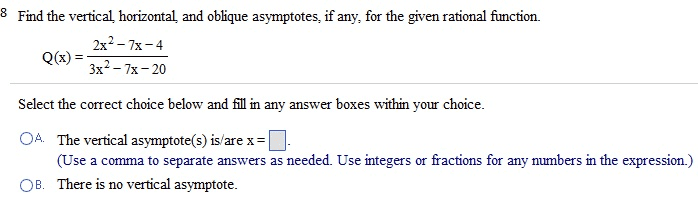
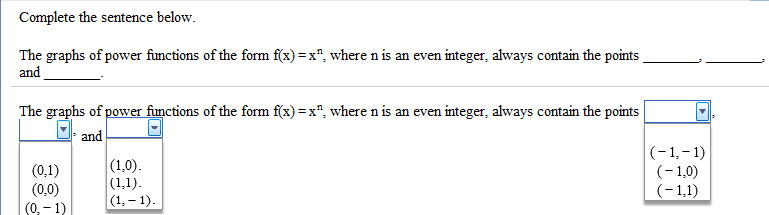MTH 99 Lecture 13: 3.4 Solving Rational Equations and Radical Equations Notes

29 views2 pages

21 Nov 2017

School

University of Miami

Department

Course

Professor

For unlimited access to Class Notes, a Class+ subscription is required.

Document Summary

Provide a generalization to each of the key terms listed in this section. Rational functions: rational functions are functions that are in the common form of r (x) = p(x) q(x) , which shows where both p(x) and q(x) are polynomial functions while it"s only q(x) can"t be a zero polynomial. Radical equations are equations that have a variable in a root square root, cubic root, etc These solutions occur when the apparent solution, after originally solving the equation, do not equal the original equations when plugged back in to check, which rechecking is the main point of solutions to con rm when dealing with radical equations. R (x) = p (x) q (x) anxn + + a1x + a0 bmxm + + b1x + b0. What is q(x)"s degree is greater than p(x)"s degree: this occurs when the denominator"s degree is larger than the numerator"s degree, m > n, horizontal asymptote: y = 0.

Related Documents

MTH 99 Lecture Notes - Lecture 18: Intermediate Value Theorem

MTH 99 Lecture Notes - Lecture 16: Polynomial

MTH 99 Chapter Notes - Chapter 5: Exponentiation, Inverse Function, Natural Logarithm

Related Questions

Algebra

Complete the sentence below. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. Complete the sentence below. The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and If r is a solution to the equation f(x) = 05 name three additional statements that can be made about f and r assuming f is a polynomial function. Choose the correct answer below. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is an x-intercept of the graph of and x - r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a complex zero of the polynomial function r is an x-intercept of the graph of and x + r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is a y-intercept of the graph of x and x + r is a factor of f. Explain what the notation Km f(x) = -infinity means. x rightarrow infinity Choose the correct answer below. The limit of f(x) as x approaches - infinity equals infinity. The limit of x as f(x) approaches infinity equals - infinity. The limit of f(x) as x approaches infinity equals - infinity. The limit of x as f(x) approaches - infinity equals infinity. Form a polynomial whose zeros and degree are given. Zeros: -7, multiplicity 1; - 3, multiplicity 2; degree 3 Type a polynomial with integer coefficients and a leading coefficient of 1 in the box below. F(x) = Find the vertical horizontal and oblique asymptotes, if any, for the following rational function.R(x) = 12x / x + 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, of the given rational function. R(x) = x3 - 64 / x2 - 6x + 8 Find the vertical asymptote(s), if any, of the function. Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Simplify your answer. Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, for the given rational function. Q(x) = 2x2 - 7x - 4 / 3x2 - 7x - 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed. Use integers or fractions for any numbers in the expression.) There is no vertical asymptote. Analyze the graph of the function. R(x) = x + 14 / x(x + 15) What is the domain of R(x)? {x x 0 andx - 16} {x x 0 andx - 16 andx - 14} {x x 0 and x - 14} All real numbers Analyze the graph of the function. R(x) = 5x + 5 / 4x + 12 What is the domain of R(x)? {x|x 0 and x -3 and x - 1} {x|x -3} {x|x and x - 3} All real numbers Analyze the graph of the function.R(x) = x2 / x2 + x - 56 What is the domain of R(x)? {x|x 7 and x - 8} {x|x 0,x -1, and x 8} {x|x 0, x 7, and x - 8} All real numbers

Show transcribed image text Complete the sentence below. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. Complete the sentence below. The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and If r is a solution to the equation f(x) = 05 name three additional statements that can be made about f and r assuming f is a polynomial function. Choose the correct answer below. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is an x-intercept of the graph of and x - r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a complex zero of the polynomial function r is an x-intercept of the graph of and x + r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is a y-intercept of the graph of x and x + r is a factor of f. Explain what the notation Km f(x) = -infinity means. x rightarrow infinity Choose the correct answer below. The limit of f(x) as x approaches - infinity equals infinity. The limit of x as f(x) approaches infinity equals - infinity. The limit of f(x) as x approaches infinity equals - infinity. The limit of x as f(x) approaches - infinity equals infinity. Form a polynomial whose zeros and degree are given. Zeros: -7, multiplicity 1; - 3, multiplicity 2; degree 3 Type a polynomial with integer coefficients and a leading coefficient of 1 in the box below. F(x) = Find the vertical horizontal and oblique asymptotes, if any, for the following rational function.R(x) = 12x / x + 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, of the given rational function. R(x) = x3 - 64 / x2 - 6x + 8 Find the vertical asymptote(s), if any, of the function. Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Simplify your answer. Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, for the given rational function. Q(x) = 2x2 - 7x - 4 / 3x2 - 7x - 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed. Use integers or fractions for any numbers in the expression.) There is no vertical asymptote. Analyze the graph of the function. R(x) = x + 14 / x(x + 15) What is the domain of R(x)? {x x 0 andx - 16} {x x 0 andx - 16 andx - 14} {x x 0 and x - 14} All real numbers Analyze the graph of the function. R(x) = 5x + 5 / 4x + 12 What is the domain of R(x)? {x|x 0 and x -3 and x - 1} {x|x -3} {x|x and x - 3} All real numbers Analyze the graph of the function.R(x) = x2 / x2 + x - 56 What is the domain of R(x)? {x|x 7 and x - 8} {x|x 0,x -1, and x 8} {x|x 0, x 7, and x - 8} All real numbers

indigosardine988