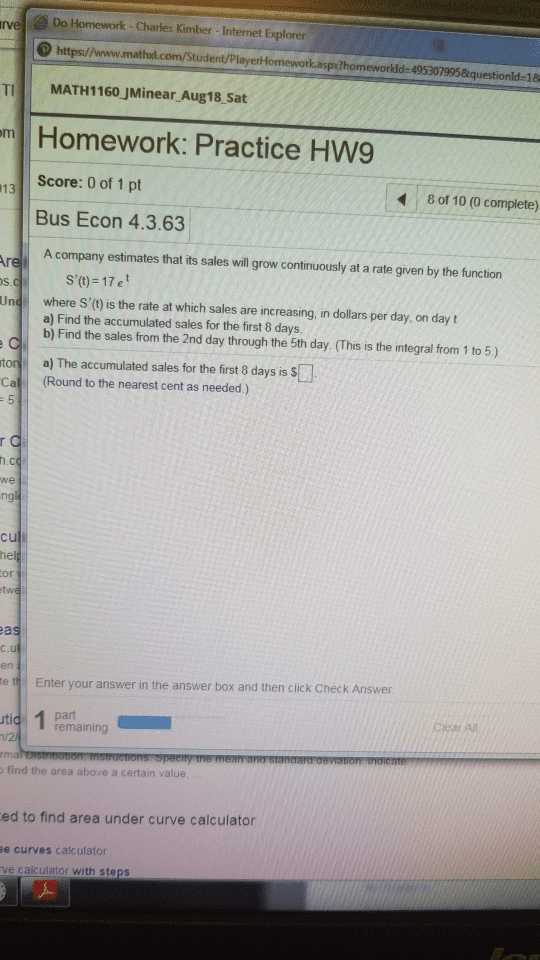
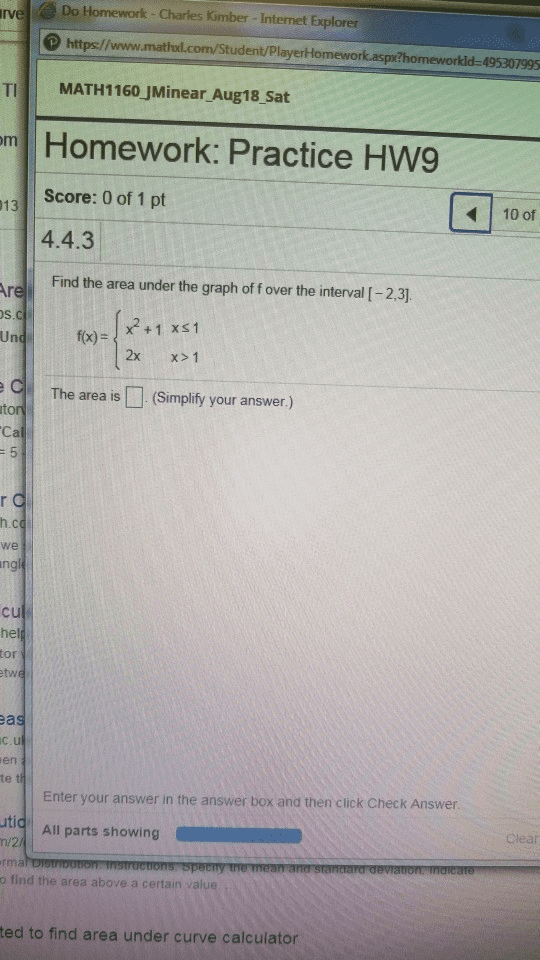
PLEASE ANSWER ALL QUESTIONS OR DO NOT ANSWER.
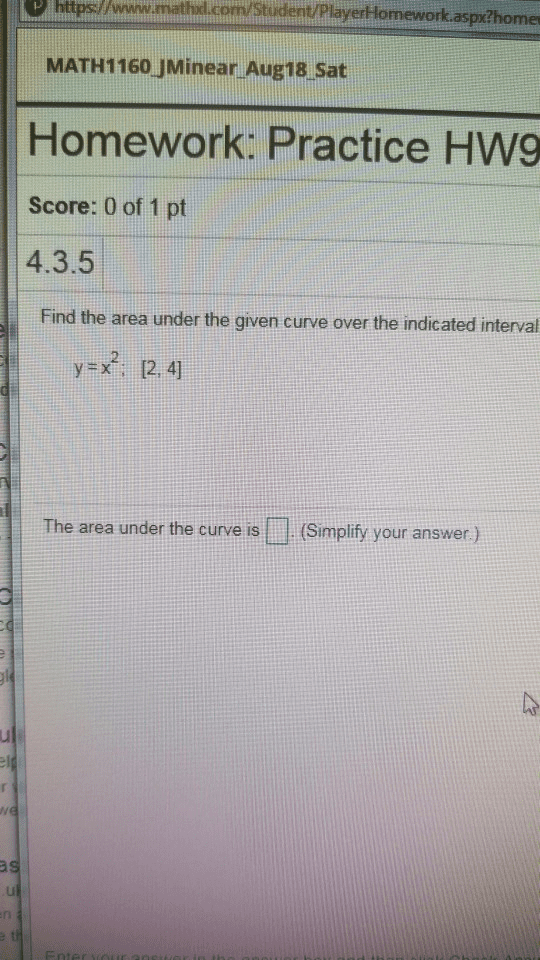
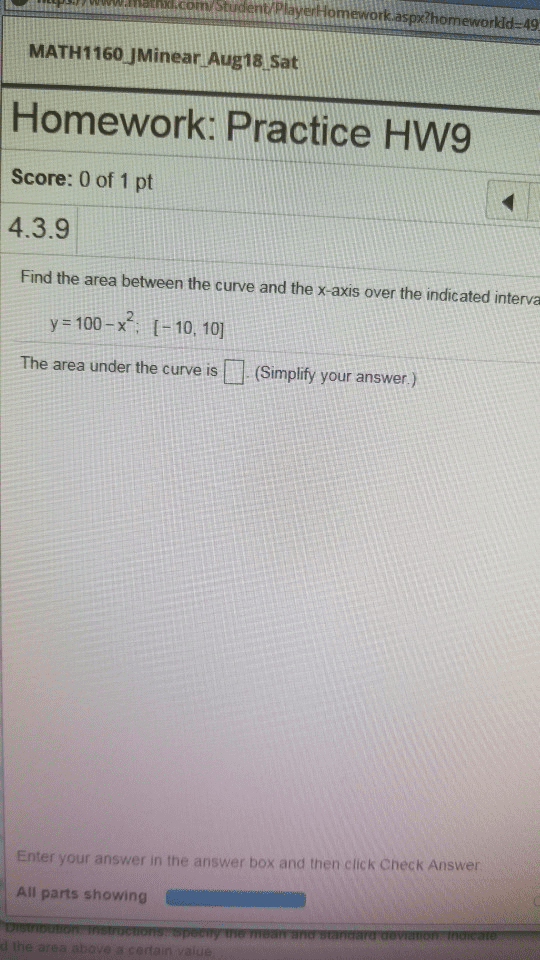
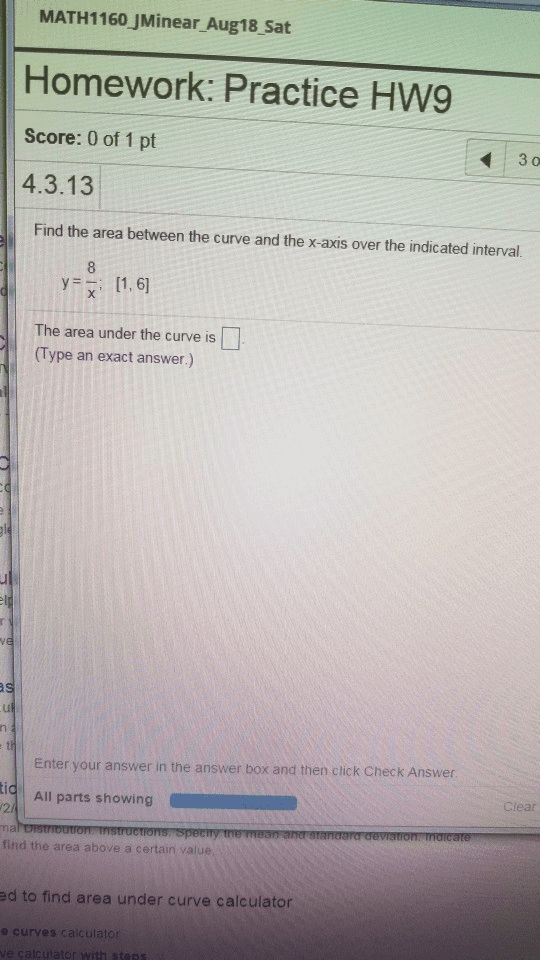
1. The formula
A = P[1 + (r/n)]^nt
Also:
Solve the logarithmic equation algebraically: Ln (X+5) = Ln (Xâ1) â Ln (X+1)
2. What is the first derivative of the following:
f(x) = ln (2x / x+1)
it is Natural Log of 2x over x+1
3. Please read the article from Money Magazine, posted in our week 8 Module, (one of my favorite financial magazines) that talks about small drop in t-bills will result in a major return in your investments (second paragraph). Why do you think that is? The article is a bit old but the question here is quite relevant about what we cover this week.
ARTICLE: Photo provided
THE ECONOMY: "Though growth averaged 2.5% stock market. says Leuthold, who recently completed a study of the stock market's daily ns over the past 100 years. In fact the stock market's daily swings from 1992 through '95 were less than half the historical average. Recently, however, daily fluctuations BY MICHAEL SIVY prices have cruised frm one high tothe next the stock market's daily swings from 1992 MosT OF THE PAST FOUR YEARS. STOCK ups and dow from one high to the next h, silent ride of a Rolls-Royce. But since March, the market has been lurching at an annual rate invest additional cash in stocks when they're low. If volatili in the first half of oyour Donailene tem dieapsirm ke a broken-down jalopy If you're hesitant to in stock prices have doubled (see the chart be- n't worry. Consider putting some be a sign that we're getting close to a market so jumpy. do of your money in long-term bonds instead. close to a mak t 1996, it will slow likely to beat stocks over the This short-term forecast doesn't change presi- the fact that the five-year outlook for stocks is terrific-thanks to the enormous underlying JTTERY AGAIN Percentage of trading days strength of the U.S. econ- the Dow moved more than 1% omy and the fact that aging -Bonds are next 12 months, says Steve Leuthold, dent of the Leuthold Group. STOCK PRICES ARE GETTING later this year.â nnpolis cuipd AGAIN advisory firm. We couldn't agree more. In fact, the out look for long-term bonds is the best it's been for more omy and the fact that agi baby boomers are continu- ing to sock away more than S20 billion a month in "The Dow couldthan a year. reach 6000 by fall but wil Here's our analysis: We see the economy slowing from its current 2.5% growth rate to only 2% or so late this year. Furthermore, stock mutual funds. Nonetheless, this is atime to restrict any new invest- ments in stocks to conserva- it makes sense to favor issues that are likely to boost their dividends, such as the shares decline ofas much as 15% starting beforea result, long-term-bond year-end." yields could sink from to day's 69% to as low as 6% by year-end. That rate decline would produce total re turns the Wall Street Newsletter n page 58. Stocks with solid around less than growth on bonds and other Income investments could return uping to fall s to 20% in the coming year. Moreover, as you sell By contrast, stocks increasingly look as some of your past year's winners, don't feel hough they are poised for a temporary 15% you have to reinvest all your profits in stocks. Consider putting some money into are likely to 30-year Treasuries (and mutual funds that start worrying that corporate profits are go- hold such long-term. high-quality issues). In hort of analysts' estimates and short, fortify your asset mix with bigger mark down share prices. "Slower earnings holdings of long-term bonds and other in- gains could turn the stock market's ail come investments such as high-yield stocks. portfo- drop in the second half of 1996. Reason: As the economy siows, investors winds into head winds." says economist That will help you keep your overall Michael SivyKathryn J. Lunstrum at Duff & Phelps in lio on track to a double-digit return even if the stock market takes a nasty 15% tumble in The tip-off that a stock market pullback the coming year. may be close is the increasing volatility o share prices over the past three months. Wall Street editor Michad Sivy is a chartered fi Volatility tends to be low in a strong, rising analyst and a former Wall Street researth director. nancia