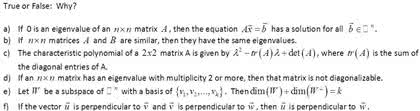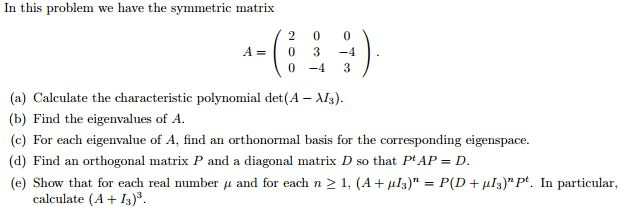MTH 114 Lecture Notes - Lecture 11: Diagonal Matrix, Diagonalizable Matrix, Matrix Decomposition
Document Summary
Scalar equation det(a - i)= 0; scalar is an eigenvalue of an nxn matrix a if and only if satisfies the characteristic equation. The number of times a factor exists in a characteristic polynomial. If nxn matrices a and b are similar, then they have the same characteristic polynomial and hence the same eigenvalues (with the same multiplicities) An nxn matrix a is diagonalizable if and only if a has n l inearly independent eigenvectors. In fact, a = pdp^-1, with d a diagonal matrix, if and only if the columns of p are n linearly independent eigenvectors of a. In this case, the diagonal entries of d are eigenvalues of a that correspond, respectively, to the eigenvectors in p. An nxn matrix with n distinct eigenvalues is diagonalizable; similar to diagonal matrix. If two matrices a and b are row equivalent, then their row spaces are the same.