HomeClass Notes1,200,000US530,000

MAC1147 Lecture 2: 6.2 Applications of Right Triangles Notes

37 views3 pages

7 Mar 2017

School

Miami Dade College

Department

Mathematics: Calculus & Pre-Calculus

Course

Professor

For unlimited access to Class Notes, a Class+ subscription is required.

Document Summary

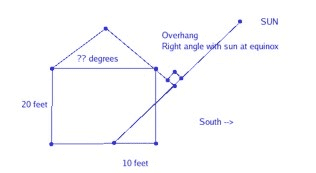
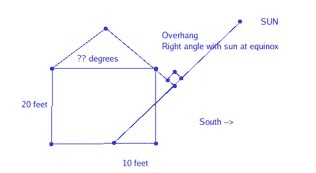
6. 2 applications of right triangles notes: sterling. Provide a generalization to each of the key terms listed in this section. In order to avoid errors when it comes to using a graphing calculator, you must [and can] store unrounded values in memory for the usage in subsequent calculations. What is true and untrue about right triangles: true. You can solve a right triangle if you know what the two sides are: untrue. You can solve a right triangle if you know what the two acute angles are. Whenever you let theta, which is , be an acute angle of any right triangle, which will explain the following functions: Cosine sin = opposite hypotenuse cos = adjacent hypotenuse. 1 y r x r b c a c. Cotangent tan = opposite adjacent y x b a csc = hypotenuse opposite sec = hypotenuse adjacent r y r x c b c a cot = adjacent opposite x y a b.

Related Documents

MAC1147 Lecture 25: 10.4 Nonlinear Systems of Equations and Inequalities Notes

MAC1147 Quiz: Review for Exam #2 Notes

MAC1147 Lecture Notes - Lecture 23: Ellipse, Unit Circle, Quadratic Equation

Related Questions

j

PLEASE NEED HELP WITH THIS TEST!!!

Use the figure below for Exercises 32-34. Find m 2 if mST = 132. Find m 4 if mRQT = 136. Find mQTS if m 1 = 27 and m 2 = 60. Classify the triangle as right, acute, or obtuse if the measures of its sides are 31, 45, and 56. Find the center and radius of the circle with equation (x + 6)2 + (x - 5)2 = 64. Find the lengths of MW- and MX-. Round your answers to the nearest tenth. Find the area of the trapezoid. Find the value of x if BD = 8 and BC = 17. Find the area of an equilateral triangle with perimeter of 60 in. Round your answer to the nearest hundredth. Find the values of x and y. Leave your answers in simplest radical form. The lengths of the sides of a right triangle are 18 ft. 24 ft. and 30 ft. What is the area of the triangle? 216 ft2 270 ft2 432 ft2 cannot be determined Find the volume of the cylinder in terms of pi. Find the value of x. Determine which of the following will tessellate. Decagon pentagon octagon triangle Determine the angle of rotation of Figure 1 to Figure 2. Figure 1 Figure 2 Given CKMS ~ DLNT. If the area of CKMS is 32 cm2, what is the area of DLNT? Find the height of a regular square prism with base edge of 6 ft and volume of 504 ft 3. What is the distance between (-12.6) and (8, -9)? Find the value of x. Assume that segments that appear to be tangent are tangent. 40 50 60 100 Find the values of x and y. If Delta DHT is similar to a triangle whose sides have lengths 4, 7, and 9. which of the following could be the perimeter of Delta DHT? 20 40 60 any of these Identify the hypothesis and conclusion of the conditional. If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment. Which of the following is the converse of the conditional in Exercise 3? If a point is congruent from the endpoints of a segment, then it is on the perpendicular bisector of the segment. If a point is equidistant from a segment, then it is on a segment perpendicular to the bisector. If a point is not on the perpendicular bisector of a segment, then it is not equidistant from the endpoints of the segment. If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment. What is the equation of a line perpendicular to that contains (4, -3)? 2x - y = 11 x - 2y = 10 2x - y = 5 x - 2y = -2 Find the length of BD. YW rightarrow bisects . Find m . Given Delta JKL ~ Delta MNP with a scale factor of 3 : 4. If Delta JKL has perimeter 57, what is the perimeter of Delta MNP? If Delta KLM Delta BCS, then which of the following is not true? Use the figure below for Exercises 10-13. Identify the pairs of angles as: alternate interior angles corresponding angles same-side interior angles vertical angles A circle has radius 17 m. Find its area and circumference to the nearest tenth. Find the coordinates of the midpoint of (9, 1) and (3, -5). Write the equation of a line in slope-intercept form that is parallel to y = - x + 8 and contains (-3 ,-5). For each pair of triangles, state the postulate or theorem you can use to prove the triangles congruent. If the triangles cannot he proven congruent, write not possible.

Show transcribed image text Use the figure below for Exercises 32-34. Find m 2 if mST = 132. Find m 4 if mRQT = 136. Find mQTS if m 1 = 27 and m 2 = 60. Classify the triangle as right, acute, or obtuse if the measures of its sides are 31, 45, and 56. Find the center and radius of the circle with equation (x + 6)2 + (x - 5)2 = 64. Find the lengths of MW- and MX-. Round your answers to the nearest tenth. Find the area of the trapezoid. Find the value of x if BD = 8 and BC = 17. Find the area of an equilateral triangle with perimeter of 60 in. Round your answer to the nearest hundredth. Find the values of x and y. Leave your answers in simplest radical form. The lengths of the sides of a right triangle are 18 ft. 24 ft. and 30 ft. What is the area of the triangle? 216 ft2 270 ft2 432 ft2 cannot be determined Find the volume of the cylinder in terms of pi. Find the value of x. Determine which of the following will tessellate. Decagon pentagon octagon triangle Determine the angle of rotation of Figure 1 to Figure 2. Figure 1 Figure 2 Given CKMS ~ DLNT. If the area of CKMS is 32 cm2, what is the area of DLNT? Find the height of a regular square prism with base edge of 6 ft and volume of 504 ft 3. What is the distance between (-12.6) and (8, -9)? Find the value of x. Assume that segments that appear to be tangent are tangent. 40 50 60 100 Find the values of x and y. If Delta DHT is similar to a triangle whose sides have lengths 4, 7, and 9. which of the following could be the perimeter of Delta DHT? 20 40 60 any of these Identify the hypothesis and conclusion of the conditional. If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment. Which of the following is the converse of the conditional in Exercise 3? If a point is congruent from the endpoints of a segment, then it is on the perpendicular bisector of the segment. If a point is equidistant from a segment, then it is on a segment perpendicular to the bisector. If a point is not on the perpendicular bisector of a segment, then it is not equidistant from the endpoints of the segment. If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment. What is the equation of a line perpendicular to that contains (4, -3)? 2x - y = 11 x - 2y = 10 2x - y = 5 x - 2y = -2 Find the length of BD. YW rightarrow bisects . Find m . Given Delta JKL ~ Delta MNP with a scale factor of 3 : 4. If Delta JKL has perimeter 57, what is the perimeter of Delta MNP? If Delta KLM Delta BCS, then which of the following is not true? Use the figure below for Exercises 10-13. Identify the pairs of angles as: alternate interior angles corresponding angles same-side interior angles vertical angles A circle has radius 17 m. Find its area and circumference to the nearest tenth. Find the coordinates of the midpoint of (9, 1) and (3, -5). Write the equation of a line in slope-intercept form that is parallel to y = - x + 8 and contains (-3 ,-5). For each pair of triangles, state the postulate or theorem you can use to prove the triangles congruent. If the triangles cannot he proven congruent, write not possible.

mauvemuskrat666

Right Triangle Trigonometry - Finding the Overhang (vernalequinox/summer solstice)

Right Triangle Trigonometry - Finding the Overhang (vernal equinox/summer solstice) A group of architects is designing a house to be built in your city. A line drawing of the house is shown below. The back of the house faces due south, and is largely windows. At 12 noon local time (this is not the same as 12 noon standard time, but is close to standard time) the sun is as high in the sky as it will be that day. On the Vernal equinox and autumnal equinox (look up these terms) the sun's highest point is 90 minus the latitude in degrees. (Why?) Â· At the summer solstice, the sun (at local noon) is about 23 degrees above the position at the equinoxes, and at the winter solstice, the sun at its highest is about 23 degrees lower than it is at the equinoxes. Since you want the winter sun (to warm up the room) and you don't want the summer sun, the house is designed to let in (most of) the winter sun, and little of the summer sun. The picture shows the sun at the Vernal equinox or autumnal equinox. The roof is pitched so that, when viewed from floor level inside the house and 10 feet in from the back wall of the house, the sun is right at the end of the overhang. In addition, the line to the sun from a point on the floor (inside the house) that is 10 feet back from the outside wall is perpendicular to the roof overhang (as shown in the line drawing). Examine the triangle whose vertices are the point 10 feet back on the floor, the point where the line to the sun intersects the back wall, and the top of the back wall.) The house is 27 feet from front to back (north to south). Find as many angles as you can. Only then use Trigonometry to find the missing distances. Find all the dimensions of the house that are not already given in the above figure at your latitude (Atlanta) at the Vernal equinox or autumnal equinox. Keeping the house the same, find all the dimensions of the house that are not already given in the above figure at your latitude (Atlanta) at the summer and winter solstices. What is the pitch of the roof? How long is the overhang?

Show transcribed image text Right Triangle Trigonometry - Finding the Overhang (vernal equinox/summer solstice) A group of architects is designing a house to be built in your city. A line drawing of the house is shown below. The back of the house faces due south, and is largely windows. At 12 noon local time (this is not the same as 12 noon standard time, but is close to standard time) the sun is as high in the sky as it will be that day. On the Vernal equinox and autumnal equinox (look up these terms) the sun's highest point is 90 minus the latitude in degrees. (Why?) Â· At the summer solstice, the sun (at local noon) is about 23 degrees above the position at the equinoxes, and at the winter solstice, the sun at its highest is about 23 degrees lower than it is at the equinoxes. Since you want the winter sun (to warm up the room) and you don't want the summer sun, the house is designed to let in (most of) the winter sun, and little of the summer sun. The picture shows the sun at the Vernal equinox or autumnal equinox. The roof is pitched so that, when viewed from floor level inside the house and 10 feet in from the back wall of the house, the sun is right at the end of the overhang. In addition, the line to the sun from a point on the floor (inside the house) that is 10 feet back from the outside wall is perpendicular to the roof overhang (as shown in the line drawing). Examine the triangle whose vertices are the point 10 feet back on the floor, the point where the line to the sun intersects the back wall, and the top of the back wall.) The house is 27 feet from front to back (north to south). Find as many angles as you can. Only then use Trigonometry to find the missing distances. Find all the dimensions of the house that are not already given in the above figure at your latitude (Atlanta) at the Vernal equinox or autumnal equinox. Keeping the house the same, find all the dimensions of the house that are not already given in the above figure at your latitude (Atlanta) at the summer and winter solstices. What is the pitch of the roof? How long is the overhang?

Show transcribed image text