HomeClass Notes1,200,000US530,000

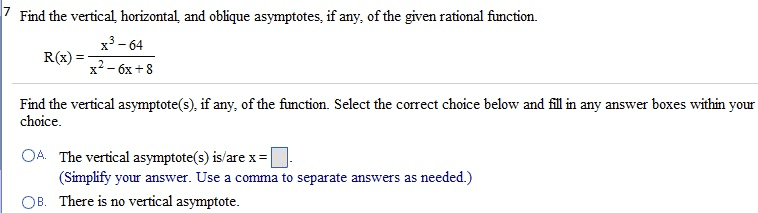
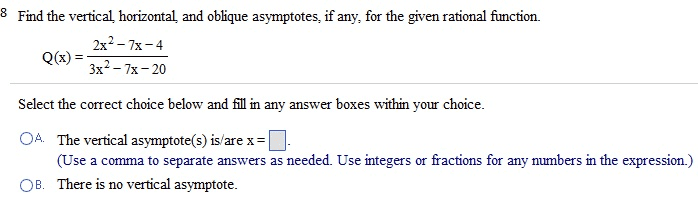
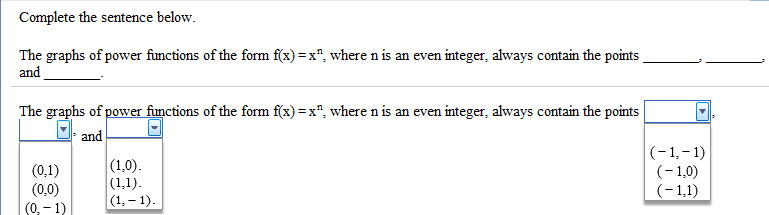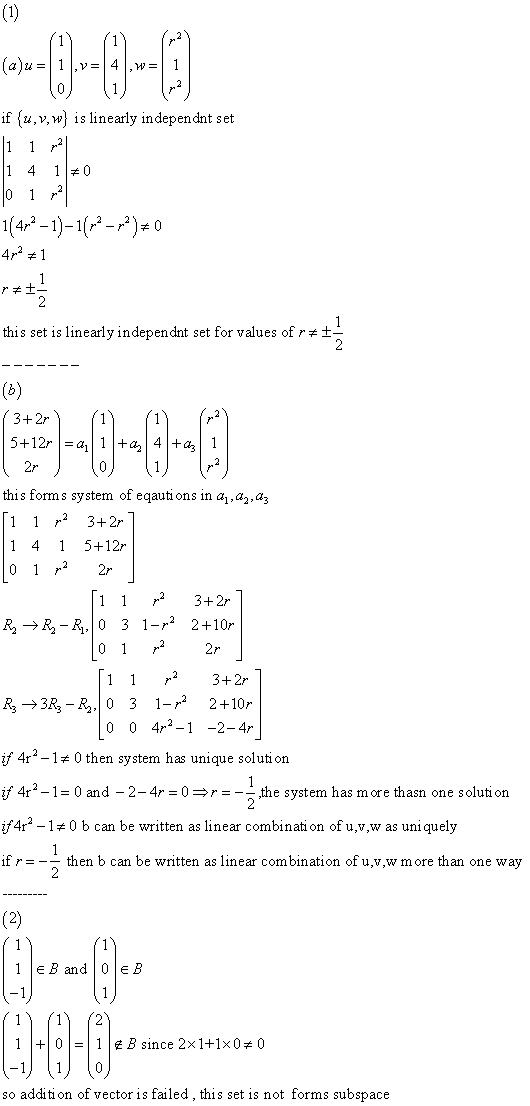MAC1105 Lecture Notes - Lecture 18: Intermediate Value Theorem, Division Algorithm

32 views3 pages

25 Feb 2017

School

Miami Dade College

Department

Mathematics: Calculus & Pre-Calculus

Course

Professor

For unlimited access to Class Notes, a Class+ subscription is required.

Document Summary

5. 2 real zeros of a polynomial function notes: sterling. Provide a generalization to each of the key terms listed in this section. = q (x) + r (x) g (x) (g (x))(cid:18) f (x) g (x)(cid:19) = (g (x))(cid:18)q (x) + r (x) g (x)(cid:19) f (x) = q (x) g (x) + r (x) If f (x) is being divided by x c, which would look like f (x) x c , then f (c) would be the remainder. The term x c would be a factor of f (x) i [if any only i ] f (c) = 0: ifthen scenario. If f (c) = 0, then x c would de nitely be a factor of f (x). If x c is a de nite factor of f (x), then f (c) = 0. A polynomial function with a degree of n has at more n real zeros, but i [if and only if] n 1.

Related Documents

MAC1105 Quiz: Review for Exam #3 Notes

MAC1105 Study Guide - Quiz Guide: Intermediate Value Theorem, Real Number

MAC1105 Study Guide - Quiz Guide: Intermediate Value Theorem, Polynomial, Real Number

Related Questions

Algebra

Complete the sentence below. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. Complete the sentence below. The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and If r is a solution to the equation f(x) = 05 name three additional statements that can be made about f and r assuming f is a polynomial function. Choose the correct answer below. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is an x-intercept of the graph of and x - r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a complex zero of the polynomial function r is an x-intercept of the graph of and x + r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is a y-intercept of the graph of x and x + r is a factor of f. Explain what the notation Km f(x) = -infinity means. x rightarrow infinity Choose the correct answer below. The limit of f(x) as x approaches - infinity equals infinity. The limit of x as f(x) approaches infinity equals - infinity. The limit of f(x) as x approaches infinity equals - infinity. The limit of x as f(x) approaches - infinity equals infinity. Form a polynomial whose zeros and degree are given. Zeros: -7, multiplicity 1; - 3, multiplicity 2; degree 3 Type a polynomial with integer coefficients and a leading coefficient of 1 in the box below. F(x) = Find the vertical horizontal and oblique asymptotes, if any, for the following rational function.R(x) = 12x / x + 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, of the given rational function. R(x) = x3 - 64 / x2 - 6x + 8 Find the vertical asymptote(s), if any, of the function. Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Simplify your answer. Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, for the given rational function. Q(x) = 2x2 - 7x - 4 / 3x2 - 7x - 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed. Use integers or fractions for any numbers in the expression.) There is no vertical asymptote. Analyze the graph of the function. R(x) = x + 14 / x(x + 15) What is the domain of R(x)? {x x 0 andx - 16} {x x 0 andx - 16 andx - 14} {x x 0 and x - 14} All real numbers Analyze the graph of the function. R(x) = 5x + 5 / 4x + 12 What is the domain of R(x)? {x|x 0 and x -3 and x - 1} {x|x -3} {x|x and x - 3} All real numbers Analyze the graph of the function.R(x) = x2 / x2 + x - 56 What is the domain of R(x)? {x|x 7 and x - 8} {x|x 0,x -1, and x 8} {x|x 0, x 7, and x - 8} All real numbers

Show transcribed image text Complete the sentence below. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. Complete the sentence below. The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and If r is a solution to the equation f(x) = 05 name three additional statements that can be made about f and r assuming f is a polynomial function. Choose the correct answer below. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is an x-intercept of the graph of and x - r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a complex zero of the polynomial function r is an x-intercept of the graph of and x + r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is a y-intercept of the graph of x and x + r is a factor of f. Explain what the notation Km f(x) = -infinity means. x rightarrow infinity Choose the correct answer below. The limit of f(x) as x approaches - infinity equals infinity. The limit of x as f(x) approaches infinity equals - infinity. The limit of f(x) as x approaches infinity equals - infinity. The limit of x as f(x) approaches - infinity equals infinity. Form a polynomial whose zeros and degree are given. Zeros: -7, multiplicity 1; - 3, multiplicity 2; degree 3 Type a polynomial with integer coefficients and a leading coefficient of 1 in the box below. F(x) = Find the vertical horizontal and oblique asymptotes, if any, for the following rational function.R(x) = 12x / x + 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, of the given rational function. R(x) = x3 - 64 / x2 - 6x + 8 Find the vertical asymptote(s), if any, of the function. Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Simplify your answer. Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, for the given rational function. Q(x) = 2x2 - 7x - 4 / 3x2 - 7x - 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed. Use integers or fractions for any numbers in the expression.) There is no vertical asymptote. Analyze the graph of the function. R(x) = x + 14 / x(x + 15) What is the domain of R(x)? {x x 0 andx - 16} {x x 0 andx - 16 andx - 14} {x x 0 and x - 14} All real numbers Analyze the graph of the function. R(x) = 5x + 5 / 4x + 12 What is the domain of R(x)? {x|x 0 and x -3 and x - 1} {x|x -3} {x|x and x - 3} All real numbers Analyze the graph of the function.R(x) = x2 / x2 + x - 56 What is the domain of R(x)? {x|x 7 and x - 8} {x|x 0,x -1, and x 8} {x|x 0, x 7, and x - 8} All real numbers

indigosardine988

I have the answer for the following question. But some of theanswers are not correct.

Please do the following question by yourself and check which arethe wrong answers,please post your answers and compare to it.

Let r in and u =(1 1 0), v = (1 4 1), w = (r2 1 r2), b = (3+2r 5+12r 2r). For which values r in is the set {u. v, w} linearly independent? For which values r in is the vector b a linear combination of u. v and w? For which of these values of r can b be written as a linear combination of u. v and w in more than one way? The set 3 of all column vectors of length three, with real entries, is a vector space. Is the subset B = {(x y z) in 3 | xy + yz = 0} a subspace of 3? Justify your answer. Show that the set of all twice differentiable functions f : satisfying the differential equation sin(x) f"(x) + x2f(x) = 0 is a vector space with respect to the usual operations of addition of functions and multiplication by scalars. Here, f" denotes the second derivative of f. Let S be the following subset of the vector space 3 of all real polynomials p of degree at most 3: S = {p in 3 | p(l) = 0, p'(l) = 0}, where p' is the derivative of p. Determine whether S is a subspace of 3. Determine whether the polynomial q(x) = x - 2x2 + x3 is an element of S. u = (1 1 0), v = (1 4 1), w = (r2 1 r2) if {u, v, w} is linearly independent set 1(4r2 - 1)-1(r2 - r2) ne 0 4r2 ne 1 r ne plusmn1/2 this set is linearly independent set for values of e ne plusmn1/2 - - - - - - - (3+2r 5+12r 2r) = a1 (1 1 0) + a2 (1 4 1) + a3 (r2 1 r2) this forms system of equations in a1, a2, a3 if 4r2 - 1 ne 0 then system has unique solution if 4r2 - 1 = 0 and -2 - 4r = 0 rArr r = -1/2, the system has more than one solution if 4r2 - 1 ne 0 b can be written as linear combination of u,v,w as uniquely if r = -1/2 then b can be written as linear combination of u,v,w more than one way - - - - - - - - - (1 1 -1) in B and (1 0 1) in B (1 1 -1) + (1 0 1) = (2 1 0) not in B since 2times1+1times0 ne 0 so addition of vector is failed, this set is not forms subspace consider the following differential equation (sinx)f"(x) + x2f (x) = 0 each solution is continuous function the set of all solutions is subset of space of set of all continuous functions n from R to R let f,g are two solutions (sinx)f"(x) + x2f (x) = 0 (sinx)g"(x)+x2g(x) = 0 ccheck whether af+bg is solution or not (sinx)f"(x) + x2f(x) = 0 rArr (sinx) af"(x) + x2?f (x) = 0 (sinx)g"(x) + x2g (x) = 0 rArr (sinx)bg" (x) + x2bg (x) = 0 (sinx)(af"(x)+bg"(x)) +x2 (af (x) + bg(x)) = 0 af+bg is also solution to differential equation the set of all solutions to differential equation forms subspace - - - - - - - - - - consider the following subset of P3 {p in P3/.p(l)=0, p'(l) = 0} let p, q in S rArr p(l)= 0, p'(l) = 0 and q(l) = 0, q'(l) = 0 (ap + bq) (l) = ap (l) +b q(l) = a (0) + b (0) = 0 (ap + bq)'(1) = ap'(l) +bq'(1) = a (0) + b(0) = 0 p, q in S rArr ap +bq in S then S is subspace q(x) = x - 2x2 + x3 q(1) = 1 - 2 + 1 = 0 q'(x)=1 - 4x + 3x2 q'(l) = 1 - 4 + 3 = 0 q is element of S