MATH 166 Lecture Notes - Lecture 4: Frustum, Plane Curve

132 views4 pages

sangriaant558

10 Feb 2018

School

Iowa State University

Department

Mathematics

Course

MATH 166

Professor

Mehmet Dagli

For unlimited access to Class Notes, a Class+ subscription is required.

Document Summary

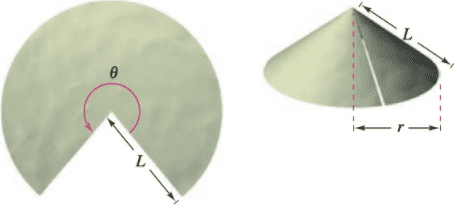
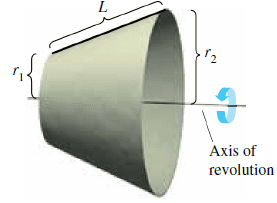
A frustum of a cone is a part of. Surface of the cone between two planes perpendicular to the axis of the cone h. Frustum e- axis of the cone a e. If a smooth plane curve y=fl on the upper part of the xy - plane is revolved about the x . axis it generates a surface of revolution y=f. 1 approximate following integrate determine partition surface the of the the area of this is to. Dse it to cut the surface into n pieces. K - th frustum is approximately equal to. The total surface area is approximately egua to. Set and up evaluate an integral for the surface area obtained by revolving the plane curve y=ti , Find the surface area of a sphere of radius r . I ytd , x=gly ) r {rrdx = 2t gly ) dlt[g"cys# dy ftp. ytzty32 generated by revolving surface ily - = 2+5,3 [ ily - tf1 } ]

Related Questions

Verifying a Formula

(a) Given a circular sector with radius L and central angle (see figure), show that the area of the sector is given by .

(b) By joining the straight-line edges of the sector in part (a), a right circular cone is formed (see figure) and the lateral surface area of the cone is the same as the area of the sector. Show that the area is , where r is the radius of the base of the cone. (Hint: The arc length of the sector equals the circumference of the base of the cone.)

(c) Use the result of part (b) to verify that the formula for the lateral surface area of the frustum of a cone with slant height L and radii r₁ and r₂ (see figure) is .(Note: This formula was used to develop the integral for finding the surface area of a surface of revolution.)