MATH 1A Lecture 11: MATH 1A - Lecture 11 - 2.7 Tangents, Rates of Change, Derivatives (February 26, 2015).docx

• School: Berkeley
• Department: Mathematics
• Course: MATH 1A
• Professor: Aganagic Mina

Document Summary

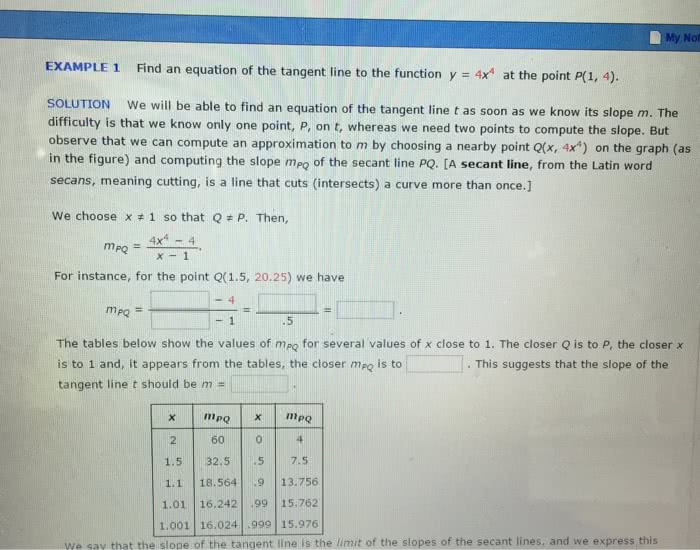
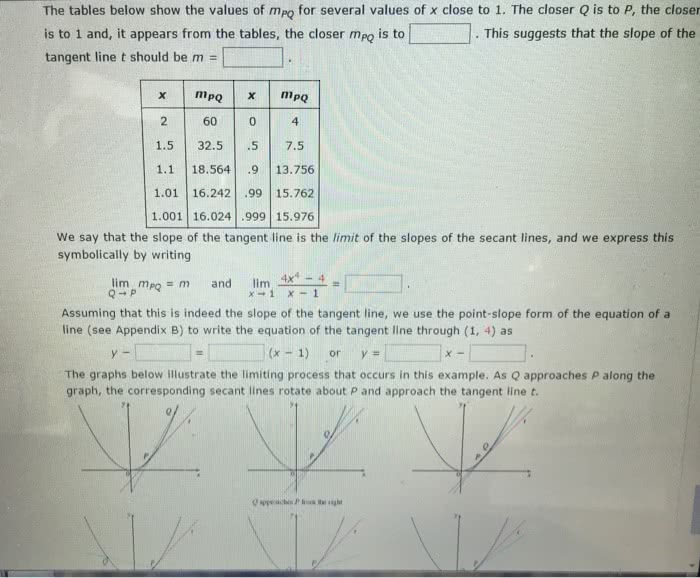
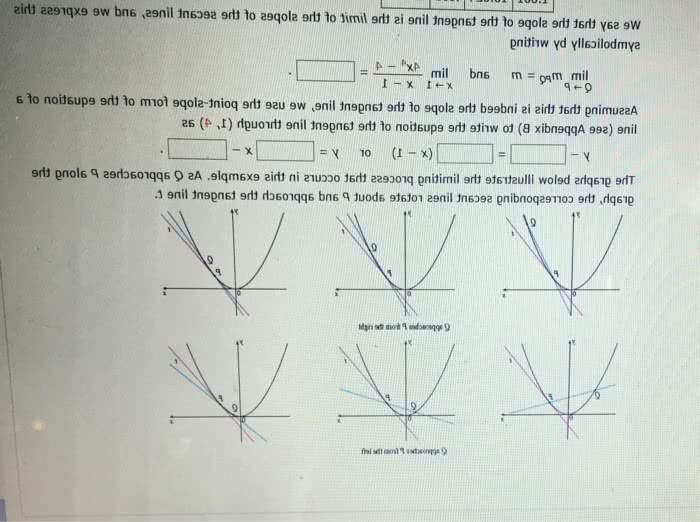
We defined limits so that we can compute slopes of tangents to curves. m = slope of tangent line at a. To do this, we compute the slope of a line that passes through a and another arbitrary point, b, which is at an arbitrary domain value x. Since a and b have coordinates (a, f(a)) and (x, f(x)), respectively. We can use this to find the slope of the tangent line at a, by taking the limit as x a. So mab = f ( x) f (a) x a lim x a. The tangent line to the curve y = f(x) at x = a is the straight line through (a, f(a)) with slope equal to: lim x a f ( x) f (a) x a. Find the tangent line to y = 2x-x2 at x = 2. To graph this, note that it can be rewritten as y = 1-(x-1)2.