Calculus 1000A/B Lecture 2: 2.1 Derivatives

• School: Western University
• Department: Calculus
• Course: Calculus 1000A/B
• Professor: Rasul Shafikov

Document Summary

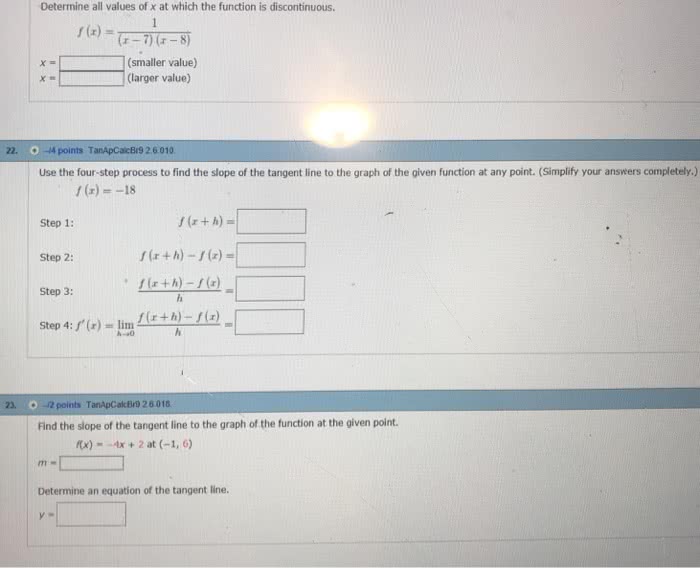
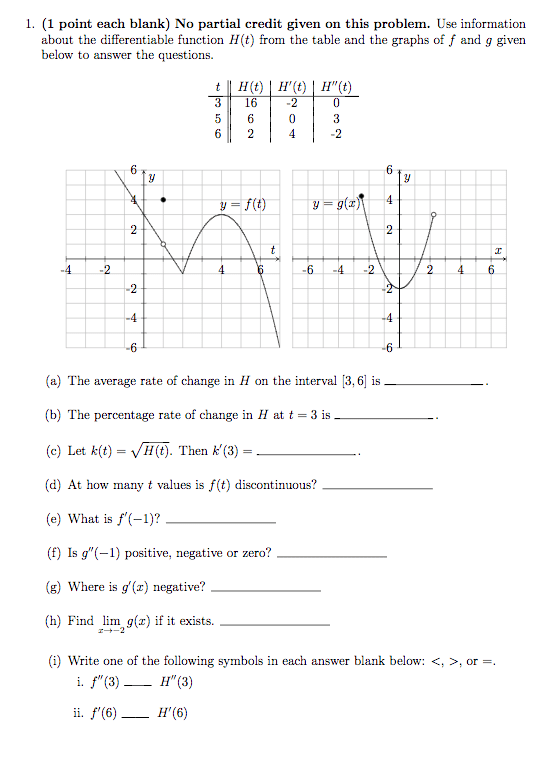
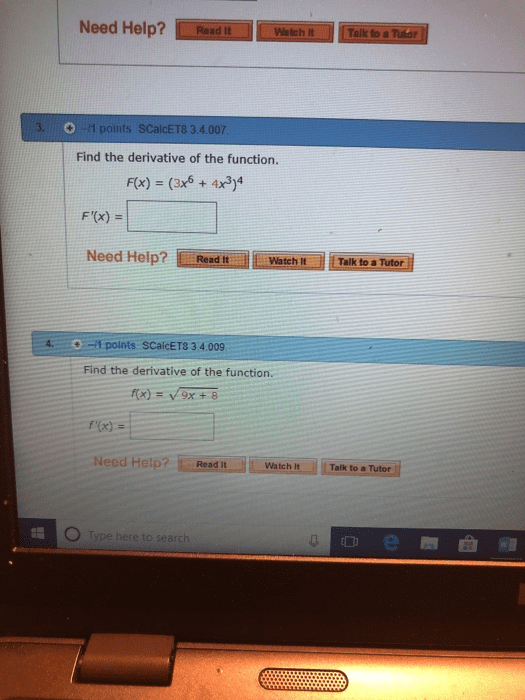
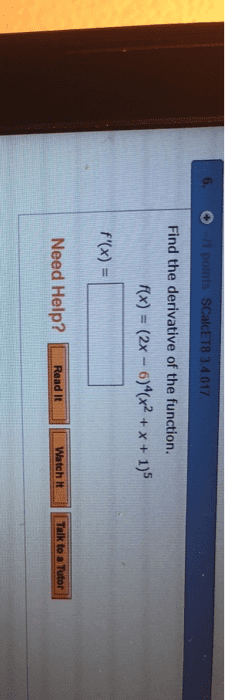
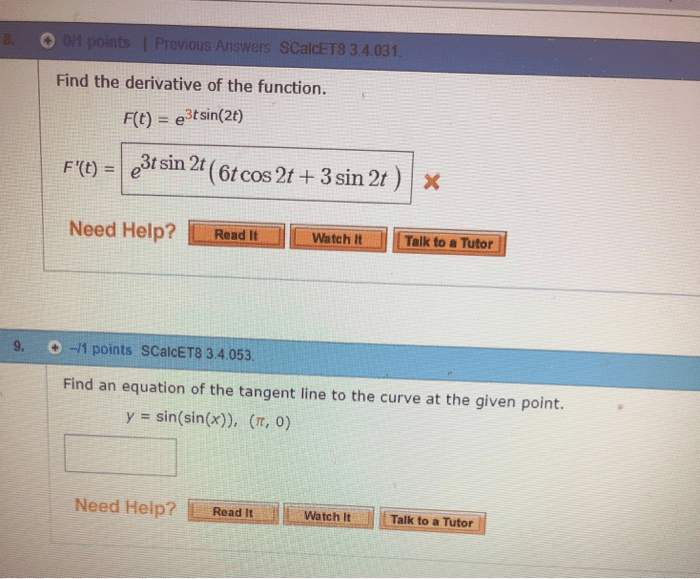
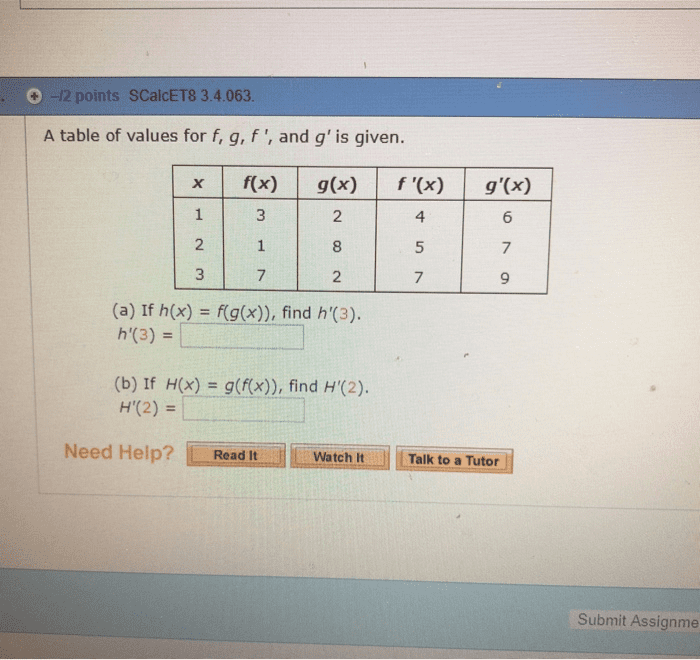
The derivative of a function f at a number a is. F (a) = lim h 0 f (a + h) f (a) h if this limit exists. Example: if f (x) = 2x 2 5x + 6 , find. F (4) = lim h 0 f (4 + h) f (4) h. Interpretations of the derivative: as the slope of the tangent. The tangent line to the curve y = f (x) at the point a, f (a) ) is the line through a, f (a) F (a) : as a rate of change. The instantaneous rate of change of y = f (x) when x = a is. For example, if s = f (t ) is the position function of a particle, then equal to v = f (t ) is the velocity of the particle at time t = a . Given a function f, the derivative of f is the function.