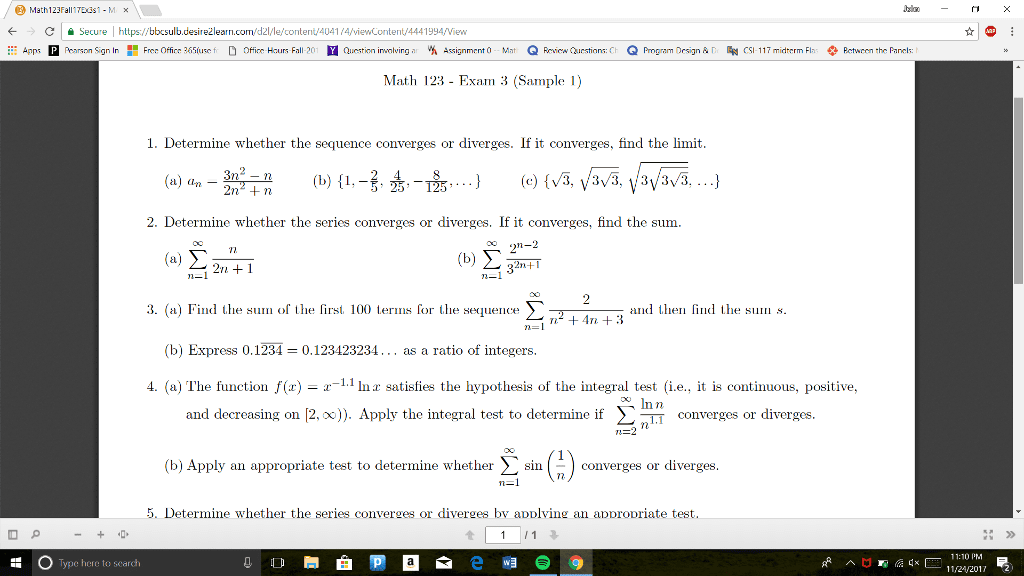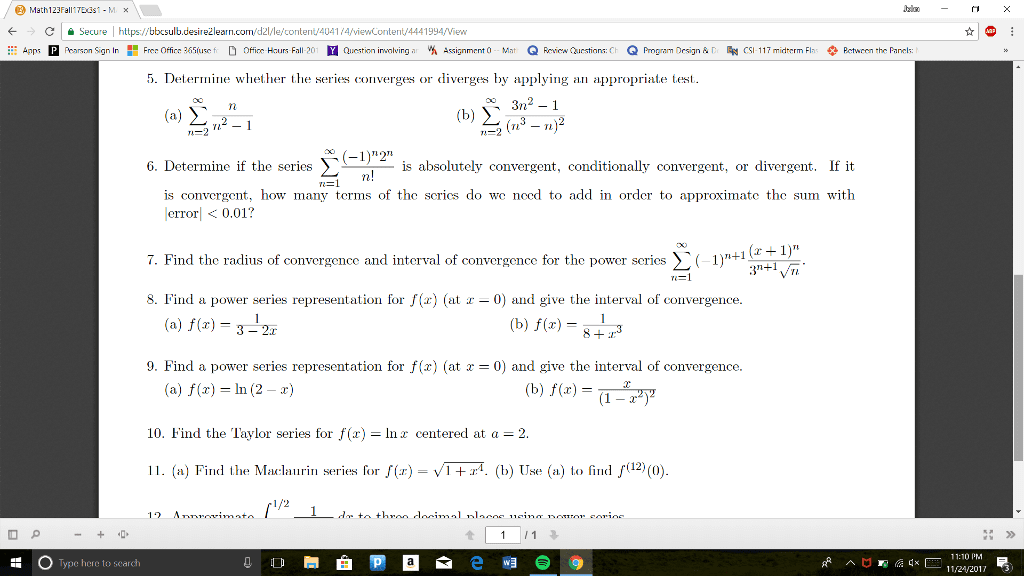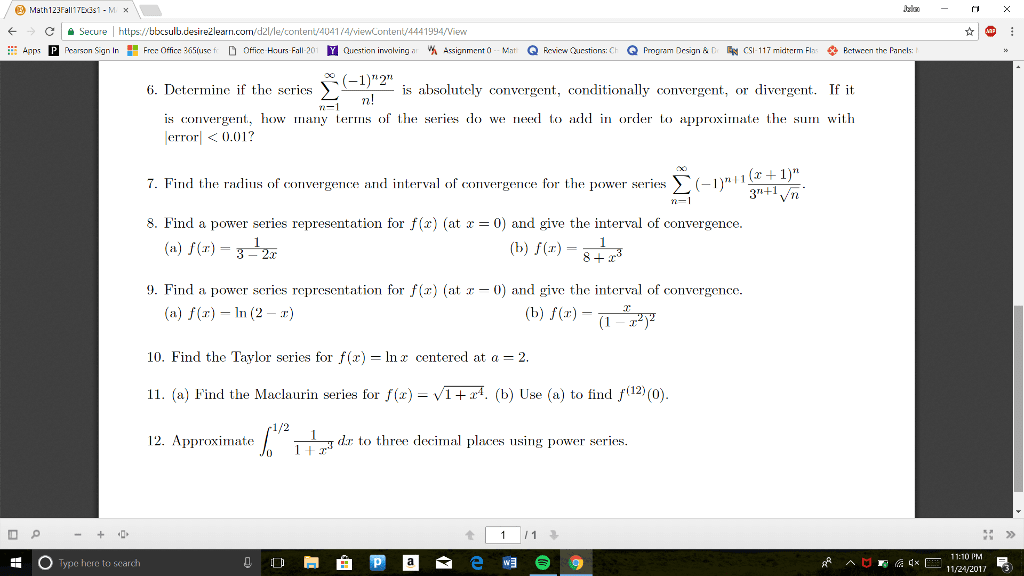MAT136H1 Lecture Notes - Lecture 4: Riemann Sum

• School: UTSG
• Department: Mathematics
• Course: MAT136H1
• Professor: Natalia Cristina Garcia Fritz

Document Summary

Mat136h1 s - lecture 4 - calculus 1(b) Example 1: express n i=1 n sin xi( = i n and i = 0,1, 2,, n as an integral. Example 2: find the reimann sum approximation for f x( ) = x 2 on 0, 2[ equal-length subintervals and right-hand endpoints for sample points. Example 3: show that i = x 2 dx b a. To find definite integral, use the equation b a f x( )dx. ] into n subintervals of equal length, of length x = at xi. , and i = 0,1, 2,, n x. A n b x n 1 x n n i=1 f xi( 2 a b a n a2 i=1 n a2 + n. ) lim n so i = lim n . S = b a n i i=1. 6 a2 + lim n a b a n + 1 n. ) 2n + 1 n2 by l"hopital"s rule, = b a.