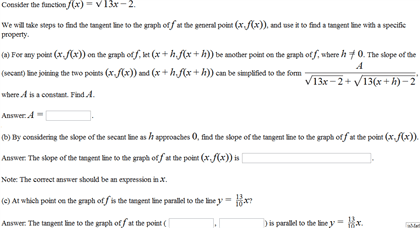MATA32H3 Lecture Notes - Lecture 4: Marginal Revenue Productivity Theory Of Wages, Marginal Revenue, Marginal Cost

53
MATA32H3 Full Course Notes
Verified Note
53 documents
Document Summary
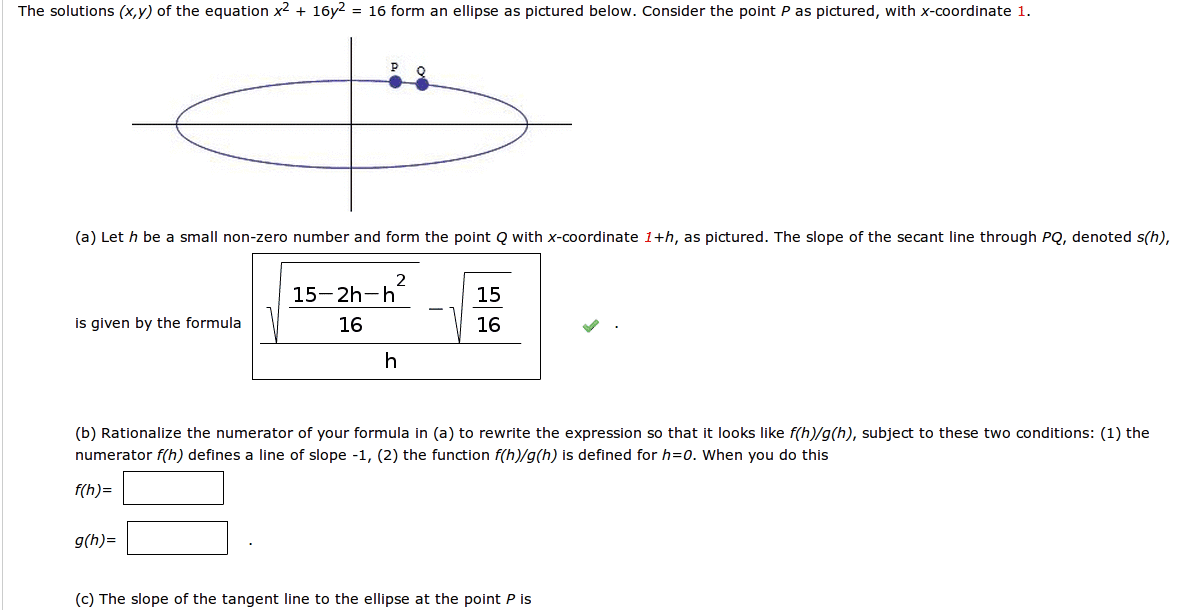
The slope of the segment line of a graph y = f(x) haf h af af. In fact as h 0, haf h. Let y = f(x). f is _____________________ if lim h. 0 haf h dy axdx exists, and the limit is called the af. The slope of the tangent line to the curve of y = f(x) at (a, f(a)) is the derivative of f at x = The derivative of y = f(x) may be denoted by dy dx y , d dx xf. Example 4. 1: let f(x) = 2x2, find the slope of the line tangent to the graph of f at the point (1, 2). Example 4. 2: is f(x) = x3 differentiable everywhere? x. The following graphs illustrate the ways in which a function can fail to be differentiable. x xf if the function has if the function has or if the function has a corner, a discontinuity, a vertical tangent.