MATH136 Lecture Notes - Lecture 27: Elementary Matrix, Invertible Matrix, If And Only If

Friday, June 30
−
Lecture 27 : Elementary matrices and invertibility. (Refers to 5.2)
Concepts:
1. Define row-equivalent matrices.
2. Recognize that a square matrix A is invertible iff A is row-equivalent to In.
3. Define elementary matrix.
4. Rank(EA) = rank(A)
5. Recognize that for any two row-equivalent matrices A and B, there exist and
invertible matrix P such that A = PB.
Recall − An ERO can always be reversed by an ERO.
- The ERO Pij can be undone by applying Pij again.
- The ERO cRj can be undone by applying (1/c)Rj .
- The ERO cRi + Rj can be undone by applying −cRi + Rj
27.1 Definition − Row-equivalent matrices. Two matrices A and B are row-equivalent if
there is a finite sequence of elementary row operations which, when applied successively,
transform the matrix A into the matrix B. We will use the notation
A ~ B
to say “A is row-equivalent to B”.
27.1.1 Example − The following chain of ERO's applied to A shows that A is row-
equivalent to B.
27.1.2 Observation − The matrix A is row-equivalent to B if and only if ARREF = BRREF.
Proof :
( ⇒ ) If A ~ B,
“A → ERO’s → B → ERO’s → BRREF” ⇒ “A → ERO’s → BRREF = ARREF”
( ⇐ ) If BRREF = ARREF,
“A → ERO’s → ARREF = BRREF → ERO’s → B” ⇒ “A → ERO’s → B”
and so A ~ B.
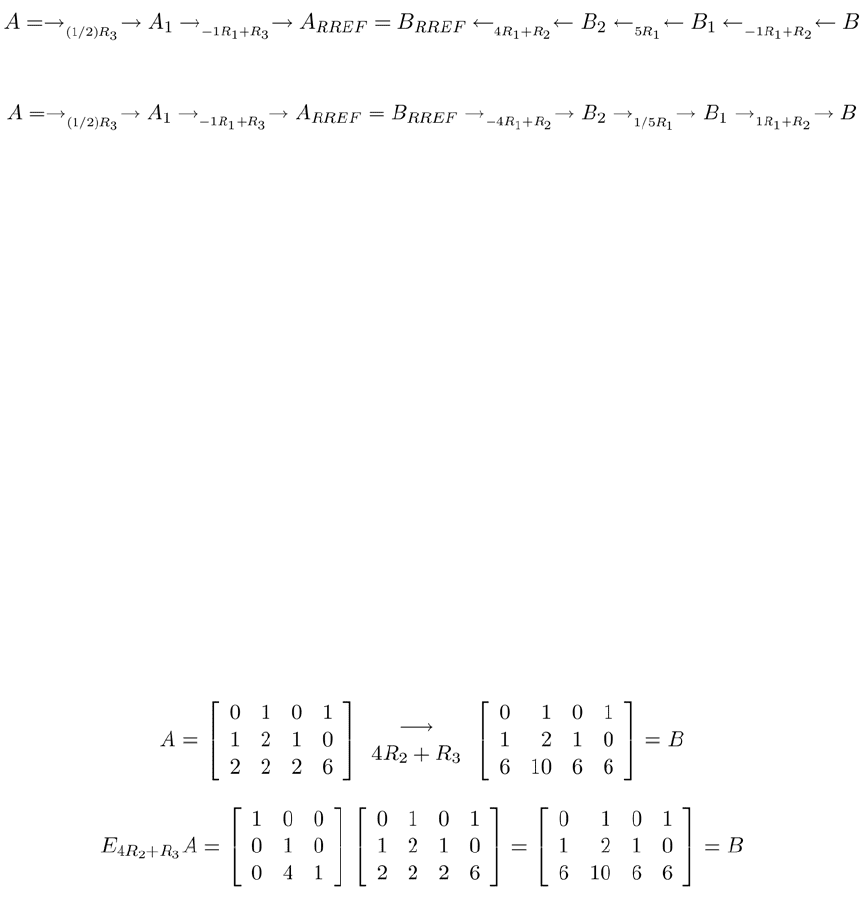
For example, if
then
27.2 Definition − An n × n elementary matrix is an n × n square matrix En × n obtained by
applying a single elementary row operation to In × n.
27.2.1 There are 3 types of elementary matrices: EPij, EcRi, EcRi + Rj. Each of these is
obtained by applying one of the 3 elementary row operations of type I, II, or II
respectively to In.
27.2.1.1 Verify this fact: Multiplying a matrix Am × n on the left by an elementary
matrix of type Ei produces the same matrix as the one obtained by applying an
elementary row operation of type i to A. That is,
- if A → Pij → B then EPij A = B,
- if A → cRi → B then EcR iA = B,
- if A → cRi + Rj → B then EcRi + Rj A = B,
27.2.1.2 Example − Compare the effect of the ERO, 4R2 + R3, on the matrix A to
the result obtained by multiplying A on the left by E4R2+ R3
27.3 Recall how an ERO can be “undone” by an ERO. (i.e. Pij undoes Pij, (1/c)Ri
undoes cRi and −cRi + Rj undoes cRi + Rj. We verify that each elementary matrix is
invertible :
- EcRi−1 = E(1/c)Ri
- EP23−1 = EP23
- EcRi + Rj−1 = E-cRi + Rj
For example

34
MATH136 Full Course Notes
Verified Note
34 documents
Document Summary
Friday, june 30 lecture 27 : elementary matrices and invertibility. (refers to 5. 2) Recall an ero can always be reversed by an ero. The ero pij can be undone by applying pij again. The ero crj can be undone by applying (1/c)rj . The ero cri + rj can be undone by applying cri + rj. Two matrices a and b are row-equivalent if there is a finite sequence of elementary row operations which, when applied successively, transform the matrix a into the matrix b. We will use the notation to say a is row-equivalent to b . 27. 1. 1 example the following chain of ero"s applied to a shows that a is row- equivalent to b. 27. 1. 2 observation the matrix a is row-equivalent to b if and only if arref = brref. Proof : ( ) if a ~ b, A ero"s b ero"s brref a ero"s brref = arref ( ) if brref = arref,

