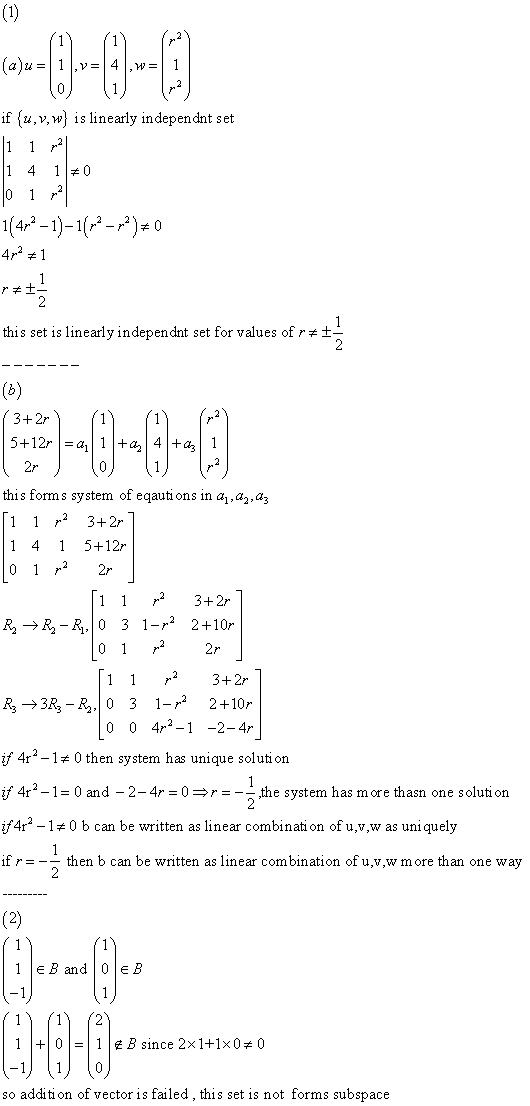HomeClass Notes1,200,000CA670,000

MATH115 Lecture 34: lect115_34_f14

20 views4 pages

scarletscorpion275

10 Oct 2015

School

University of Waterloo

Department

Course

Professor

For unlimited access to Class Notes, a Class+ subscription is required.

Document Summary

Friday, november 21 lecture 34: linear independence - finite dimensional vector spaces. Expectations: define a linear independent set of vectors, find the basis and dimension of simple abstract vector spaces. Let v1, v2, , vk be k vectors in the vector space v. the vectors v1, v2, . ,vk are said to be linearly independent if the only way that. 1v1 + 2v2 + + kvk = 0 can hold is if 1, 2 , k are all zeroes. , vk are not linearly independent, i. e. there exists 1, 2 , k not all. Zero such that 1v1 + 2v2 + + kvk = 0, then they are said to be linearly dependent. 34. 2 example of a set in m 2 x 2 which is not linearly independent. These are not linearly independent since a + 2b c = 0. (where 0 is the zero matrix. )

Related textbook solutions

Calculus

ISBN: 9781319050733

Single Variable Calculus: Early Transcendentals

4th Edition, 2018

ISBN: 9781337687805

CALCULUS:EARLY TRANSCENDENTALS

ISBN: 9781319050740

Related Documents

MATH115 Lecture Notes - Lecture 28: Linear Combination, Orthogonal Matrix

scarletscorpion275

MATH115 Lecture Notes - Lecture 30: Aomedia Video 1, Orthogonalization, Linear Combination

scarletscorpion275

MATH115 Lecture 27: lect115_27_f14

scarletscorpion275

Related Questions

Show transcribed image text

carminebeaver663

I have the answer for the following question. But some of theanswers are not correct.

Please do the following question by yourself and check which arethe wrong answers,please post your answers and compare to it.

Let r in and u =(1 1 0), v = (1 4 1), w = (r2 1 r2), b = (3+2r 5+12r 2r). For which values r in is the set {u. v, w} linearly independent? For which values r in is the vector b a linear combination of u. v and w? For which of these values of r can b be written as a linear combination of u. v and w in more than one way? The set 3 of all column vectors of length three, with real entries, is a vector space. Is the subset B = {(x y z) in 3 | xy + yz = 0} a subspace of 3? Justify your answer. Show that the set of all twice differentiable functions f : satisfying the differential equation sin(x) f"(x) + x2f(x) = 0 is a vector space with respect to the usual operations of addition of functions and multiplication by scalars. Here, f" denotes the second derivative of f. Let S be the following subset of the vector space 3 of all real polynomials p of degree at most 3: S = {p in 3 | p(l) = 0, p'(l) = 0}, where p' is the derivative of p. Determine whether S is a subspace of 3. Determine whether the polynomial q(x) = x - 2x2 + x3 is an element of S. u = (1 1 0), v = (1 4 1), w = (r2 1 r2) if {u, v, w} is linearly independent set 1(4r2 - 1)-1(r2 - r2) ne 0 4r2 ne 1 r ne plusmn1/2 this set is linearly independent set for values of e ne plusmn1/2 - - - - - - - (3+2r 5+12r 2r) = a1 (1 1 0) + a2 (1 4 1) + a3 (r2 1 r2) this forms system of equations in a1, a2, a3 if 4r2 - 1 ne 0 then system has unique solution if 4r2 - 1 = 0 and -2 - 4r = 0 rArr r = -1/2, the system has more than one solution if 4r2 - 1 ne 0 b can be written as linear combination of u,v,w as uniquely if r = -1/2 then b can be written as linear combination of u,v,w more than one way - - - - - - - - - (1 1 -1) in B and (1 0 1) in B (1 1 -1) + (1 0 1) = (2 1 0) not in B since 2times1+1times0 ne 0 so addition of vector is failed, this set is not forms subspace consider the following differential equation (sinx)f"(x) + x2f (x) = 0 each solution is continuous function the set of all solutions is subset of space of set of all continuous functions n from R to R let f,g are two solutions (sinx)f"(x) + x2f (x) = 0 (sinx)g"(x)+x2g(x) = 0 ccheck whether af+bg is solution or not (sinx)f"(x) + x2f(x) = 0 rArr (sinx) af"(x) + x2?f (x) = 0 (sinx)g"(x) + x2g (x) = 0 rArr (sinx)bg" (x) + x2bg (x) = 0 (sinx)(af"(x)+bg"(x)) +x2 (af (x) + bg(x)) = 0 af+bg is also solution to differential equation the set of all solutions to differential equation forms subspace - - - - - - - - - - consider the following subset of P3 {p in P3/.p(l)=0, p'(l) = 0} let p, q in S rArr p(l)= 0, p'(l) = 0 and q(l) = 0, q'(l) = 0 (ap + bq) (l) = ap (l) +b q(l) = a (0) + b (0) = 0 (ap + bq)'(1) = ap'(l) +bq'(1) = a (0) + b(0) = 0 p, q in S rArr ap +bq in S then S is subspace q(x) = x - 2x2 + x3 q(1) = 1 - 2 + 1 = 0 q'(x)=1 - 4x + 3x2 q'(l) = 1 - 4 + 3 = 0 q is element of S