MATH 1M03 Lecture Notes - Lecture 5: Product Rule
22 Feb 2016
School
Department
Course
Professor
Document Summary
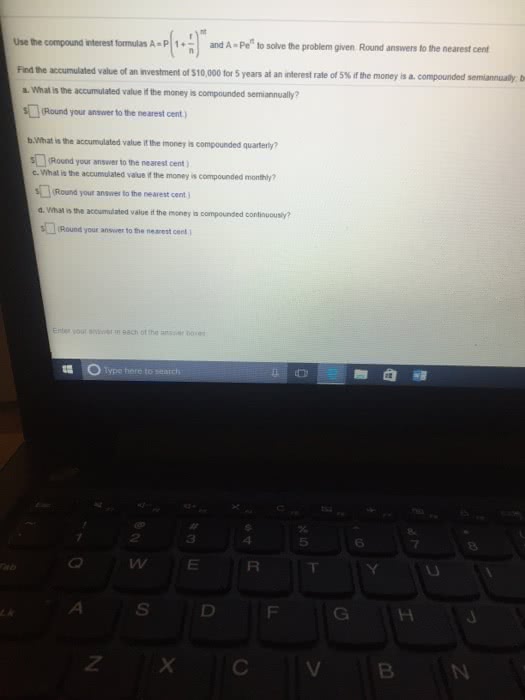
If we write b(t) to be the accumulated balance at the time t, we have. = ln 2 = rt t = ln 2 r. Notice that the estimate above is independent of the value p. Suppose an investment p is compounded continuously with an annual interest rate r . Again, let b(t) to be the accumulated balance at time t. we have. If the balance at time t equals to q, then. = ln q ln p = rt t = ln q ln p r. Suppose an investment p is compounded k times a year with an annual interest rate r . Let b(t) to be the accumulated balance at time t. if b(t) = q, we have. Q = b(t) = p(cid:16)1 + r k(cid:17)kt. P(cid:19) = ln(cid:18)(cid:16)1 + r k(cid:17)kt(cid:19) ln q ln p = kt ln(cid:16)1 + r k(cid:17) t = ln q ln p k ln(cid:0)1 + r k(cid:1)
